Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi chiều dài mảnh vườn là a(m)
Khi đó ta có \(2a + 2x = 40 \Leftrightarrow a = 20 - x\)
Vậy diện tích mảnh vườn hình chữ nhật là: \(S = a.x = (20 - x)x = - {x^2} + 20x\)
b) Để diện tích mảnh vườn lớn nhất thì S phải lớn nhất:
Ta có \(S = - {x^2} + 20x = - ({x^2} - 20x + 100) + 100 = 100 - {(x - 10)^2} \le 100\)(vì \({(x - 10)^2} \ge 0\))
Diện tích mảnh vườn lớn nhất là 100 \(\left( {{m^2}} \right)\) khi x = 10

a) Diện tích một phần tư hình tròn là: \(\frac{1}{4}\pi {r^2}\)
Gọi x là biến số thể hiện kích thước của bán kính.
Công thức hàm số tính diện tích bồn hoa là: \(f(x) = \frac{1}{4}\pi {x^2}\)
+) Vì bán kính bồn hoa có kích thước từ 0,5 m đến 3 m nên \(0,5 \le x \le 3\)
Vậy tập xác định của hàm số này là \(D = [0,5;3]\)
b) Diện tích là \(0,5\pi \;{m^2}\) tức là\(f(x) = 0,5\pi \;\)
\( \Leftrightarrow \frac{1}{4}\pi {x^2} = 0,5\pi \Leftrightarrow {x^2} = 2 \Rightarrow x = \sqrt 2 \) (do \(0,5 \le x \le 3\))
Vậy bán kính bồn hoa bằng \(\sqrt 2 \;m\).

Theo giải thiết ta có tam thức sau: \(f\left( x \right) = 20.15 - \left( {20 + x} \right)\left( {15 - x} \right) = {x^2} + 5x\)
Tam thức có \(\Delta = 25 > 0\), có hai nghiệm phân biệt \({x_1} = 0;{x_2} = -5\)
Vậy khoảng diện tích tăng lên là \(x>0\) và \(x<-5\), khoảng diện giảm đi là \(x \in(-5;0)\) và diện tích không đổi khi \(x = 0\) và \(x = -5\)

Gọi x là chiều rộng của vườn hoa (\(x > 0\), tính bằng đơn vị mét)
Theo giả thiết ta có chiều dài là \(15 - x\)
Diện tích của vườn hoa có phương trình như sau \(f\left( x \right) = x\left( {15 - x} \right) = - {x^2} + 15x\)
Ta có bất phương trình thỏa mãn bài toán như sau:\( - {x^2} + 15x \ge 50 \Leftrightarrow - {x^2} + 15x - 50 \ge 0\)
Xét tam thức \(g\left( x \right) = - {x^2} + 15x - 50\) có hai nghiệm phân biệt là \({x_1} = 5;{x_2} = 10\) và \(a = - 1 < 0\) nên \(g\left( x \right) > 0\) khi x thuộc đoạn \(\left[ {5;10} \right]\)
Vậy khi chiều rộng nằm trong đoạn \(\left[ {5;10} \right]\) mét thì diện tích vườn hoa ít nhất là 50 \({m^2}\).

Đáp án: D
Gọi chiều dài, chiều rộng của mảnh vườn lần lượt là ![]() (m)
(m) ![]()
Theo đề bài ta có:  là nghiệm của phương trình
là nghiệm của phương trình ![]()

Đáp án: A
Gọi chiều dài, chiều rộng của mảnh vườn lần lượt là ![]() (m)
(m) ![]()
Theo đề bài ta có:
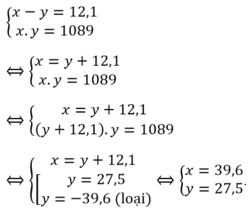

Từ giải thiết ta có: \(2a = 80 \Rightarrow a = 40,2b = 40 \Rightarrow b = 20\)
Suy ra, \(c = \sqrt {{a^2} - {b^2}} = 20\sqrt 3 \)
Suy ra vị trí đinh cách mép là \(a - c = 40 - 20\sqrt 3 = 5,36\) cm
Chiều dài vòng dây là \(2a + 2c = 2.40 + 2.20\sqrt 3 = 149,28\) cm
Vậy phải ghim hai cái đinh cách các mép tấm bìa 5,36 cm và lấy vòng dây có độ dài là 149,28 cm