Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều dài, chiều rộng của mảnh vườn hình chữ nhật lần lượt là x (m), y (m). (điều kiện x > y > 0)
a) Theo đề bài:
Chu vi là 94,4m nên ta có phương trình: 2(x + y) = 94,4 (1)
Diện tích là 494,55m2 nên ta có phương trình: x.y = 494,55 (2)
Từ (1) và (2) ta có hệ:
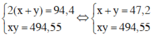
Giải hệ phương trình trên:
Cách 1: Dựa vào định lý Vi–et đảo
Từ hệ phương trình suy ra x, y là nghiệm của phương trình:
X2 – 47,2X + 494,55 = 0
Giải phương trình ta được: X1 = 31,5 và X2 = 15,7
Vì x > y nên x = 31.5 và y = 15.7
Cách 2: Phương pháp thế
Từ x + y = 47,2 ⇒ x = 47,2 – y, thay vào phương trình x.y = 494,55 ta được:
(47,2 – y).y = 494,55
⇔ 47,2.y – y2 = 494,55
⇔ y2 – 47,2y + 494,55 = 0
⇔ y = 31.5 hoặc y = 15.7
Nếu y = 31.5 ⇒ x = 15.7 (loại vì x < y)
Nếu y = 15.7 ⇒ x = 31.5 (thỏa mãn).
Vậy hình chữ nhật có chiều dài bằng 31.5m và chiều rộng bằng 15.7m
b) Theo đề bài:
Hiệu của hai cạnh là 12,1 m nên ta có phương trình: x – y = 12,1 (3)
Diện tích là 1089m2 nên ta có phương trình: x.y = 1089 (4)
Từ (3) và (4) ta có hệ: 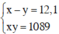
Từ (3) ⇒ x = 12,1 + y, thay vào (4) ta được:
(12,1 + y).y = 1089
⇔ y2 + 12,1.y – 1089 = 0
⇔ y = 27,5 (t/m) hoặc y = –39,6 (loại)
⇒ x = 12,1 + 27,5 = 39,6
Vậy hình chữ nhật có chiều dài 39,6m và chiều rộng 27,5m

Đáp án: D
Gọi chiều dài, chiều rộng của mảnh vườn lần lượt là ![]() (m)
(m) ![]()
Theo đề bài ta có:  là nghiệm của phương trình
là nghiệm của phương trình ![]()

Gọi chiều rộng là x
Chiều dài là x+6
Theo đề, ta có: 4(x+6)-x=51
=>4x+24-x=51
=>3x+24=51
=>x=9
Chiều dài là 9+6=15(m)
Chu vi là (15+9)x2=48(m)
Diện tích là 15x9=135(m2)

Chiều rộng bằng: \(\frac{2}{7}\) : 40% = \(\frac{5}{7}\) chiều dài
Chiều rộng hình chữ nhật là: 70 . \(\frac{5}{7}\) = 50 (m)
Chu vi hình chữ nhật là: (70 + 50) . 2 = 240 (m)
Diện tích hình chữ nhật là: 70 . 50 = 3500 (m2)
40% củ chiều rộng là:
70*\(\frac{2}{7}\)=20(m)
chiều rộng của miếng đất là:
20:40*100=20(m)
chu vi miếng đất là:
(70+50)*2=240(m)
Diện tích miếng đất là:
70*20=1400(m2)
Đáp số :chu vi 240m
diện tích 1400m2
Lạy trờ phật co em dc 1GB

Gọi x là chiều rộng của vườn hoa (\(x > 0\), tính bằng đơn vị mét)
Theo giả thiết ta có chiều dài là \(15 - x\)
Diện tích của vườn hoa có phương trình như sau \(f\left( x \right) = x\left( {15 - x} \right) = - {x^2} + 15x\)
Ta có bất phương trình thỏa mãn bài toán như sau:\( - {x^2} + 15x \ge 50 \Leftrightarrow - {x^2} + 15x - 50 \ge 0\)
Xét tam thức \(g\left( x \right) = - {x^2} + 15x - 50\) có hai nghiệm phân biệt là \({x_1} = 5;{x_2} = 10\) và \(a = - 1 < 0\) nên \(g\left( x \right) > 0\) khi x thuộc đoạn \(\left[ {5;10} \right]\)
Vậy khi chiều rộng nằm trong đoạn \(\left[ {5;10} \right]\) mét thì diện tích vườn hoa ít nhất là 50 \({m^2}\).

Đáp án: C
Gọi cạnh lớn, cạnh bé của mảnh vườn lần lượt là b, a (m) (b > a > 0)
Theo đề bài ta có: a + b = 11 a . b = 24
=> a,b là nghiệm của phương trình:
X2 – 11X + 24 = 0 => a=3, b=8

Chu vi hình chữ nhật là :
12 x 4 = 48 (m)
Nửa chu vi hình chữ nhật là :
48 : 2 = 24 (m)
Chiều rộng hình chữ nhật là :
24 - 16 = 8 (m)
Diện tích hình chữ nhật là :
24 x 8 = 192 (m2)
Đáp án : 192m2
Nua chu vi HCN:
12 x 4 : 2 = 24 (m)
Chieu rong HCN:
24 - 16 = 8 (m)
Dien tich HCN:
24 x 8 = 192 (m2)

Đáp án: A
Gọi chiều dài, chiều rộng của mảnh vườn lần lượt là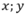 (m)
(m) 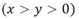
Theo đề bài ta có: