ZO
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TH
7 tháng 12 2021
a) Ta có: đường kính AB vuông góc với dây CD tại M (gt) (1)
⇒MC=MD(2)⇒MC=MD(2)
Mà MA = ME (E đối xứng với A qua M) (3)
Từ (2), (3) ⇒⇒ Tứ giác ACED là hình bình hành (4)
Từ (1), (2) ⇒AB⇒AB là đường trung trực của CD
⇒⇒ Điểm E nằm trên đường trung trực AB cách đều 2 đầu mút C và D ⇒EC=ED⇒EC=ED (5)
Từ (4), (5) ⇒⇒ Tứ giác ACED là hình thoi
b) Ta có: AB = 2R = 2 . 6,5 = 13 (cm)
⇒MB=AB−MA=13−4=9(cm)⇒MB=AB−MA=13−4=9(cm)
Theo hệ thức lượng ta có:
MC2 = MA . MB = 4 . 9 = 36
⇔MC=√36=6(cm)⇔MC=36=6(cm)
Từ (2) ⇒MC=MD=CD2⇒MC=MD=CD2
⇔CD=2MC=2.6=12(cm)
em mới học lớp 5 ạ
. Biết chiều rộng của khúc sông đó là 300m.
TM
21 tháng 7 2023
chứng minh: \(1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
xét VT: \(1+tg^2\alpha=1+\dfrac{sin^2\alpha}{cos^2\alpha}\left(vì:tg\left(\alpha\right)=\dfrac{sin\left(\alpha\right)}{cos\left(\alpha\right)}\right)\)
\(=\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}=\dfrac{1}{cos^2\alpha}\left(vì:sin^2\alpha+cos^2\alpha=1\right)=VP\Rightarrow1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
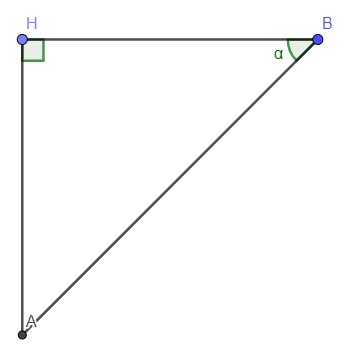
\(\Leftrightarrow1+\dfrac{AH^2}{50^2}=\dfrac{1}{\left(\dfrac{AH^2}{AB^2}\right)}=\dfrac{AB^2}{AH^2}\Leftrightarrow\dfrac{2500+AH^2}{2500}=\dfrac{AB^2}{AH^2}\Leftrightarrow2500AH^2+AH^4=2500AB^2\left(1\right)\)
ta có: \(AH^2+BH^2=AB^2\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow2500AH^2+AH^4=2500\left(AH^2+50^2\right)\Leftrightarrow AH^4=2500.2500=50^4\Leftrightarrow AH=50\left(m\right)\left(3\right)\)
\(\left(2\right)\left(3\right)\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{50^2+50^2}=50\sqrt{2}\left(m\right)\)
vậy chiều rộng con sông là: \(AH=50\left(m\right)\) và quãng đường đò đã đi là \(AB=50\sqrt{2}\left(m\right)\)
NH
16 tháng 3 2020
Lần 1 người đó lãi 12-10=2(triệu)
Lần 2 mua lại lãi:12-15=-3(triệu)
Lần 3 bán con bò lãi : 17-15=2triệu (so vs khi mua lại con bò )
So với khi mua con bò vs giá 10 triệu , người đó lãi số tiền là : -3 - 2= -1 ( triệu )
Vì -1 là số âm nên người đó đã lỗ 1 triệu đồng
con kiến cõng con của nó bò qua sông
con kien cong con cua no qua song