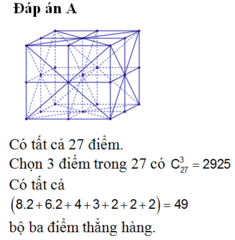
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
Để khối lập phương nhỏ thu được sau khi cắt có có đúng 2 mặt được sơn đỏ thì khối lập phương nhỏ đó phải có một cạnh nằm trên cạnh giao của hai mặt hình lập phương, mà tại các đỉnh thì khối lập phương nhỏ thu được sẽ có 3 mặt được tô đỏ.
=> trên một cạnh của hình lập phương ta sẽ có có 8 khối lập phương nhỏ thỏa mãn đề. Vì hình lập phương có tất cả 12 cạnh nên số khối lập phương thu được sau khi cắt có đúng 2 mặt được sơn đỏ là 8.12=96.
Chọn D
Mỗi mặt của khối lập phương chứa 4 mặt của 4 khối lập phương nhỏ chỉ có 1 mặt được sơn đỏ Vậy số khối lập phương chỉ có 1 mặt được sơn đỏ là 4x6=24.
Đáp án:A
Hướng dẫn giải:
Gọi a là độ dài cạnh của hình lập phương
⇒ sau khi tăng thì độ dài là a + 2.
Ta có ( a + 2 ) 3 - a 3 = 98
⇔ 6 a 2 + 12 a - 90 = 0
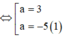
Chọn D.
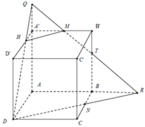
Dễ thấy A'A, B'M, D'N đồng quy tại S, SA' = 2a. Từ đó, ta tính được V S . A ' B ' D ' và V S . AMN . Suy ra tính được V H
Chọn B
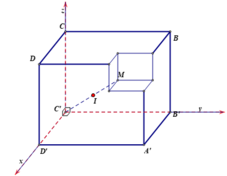
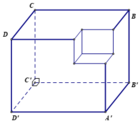
Gọi M là đỉnh của hình lập phương có cạnh bằng 1 nằm trên đường chéo AC' và nằm trên khối còn lại sau khi cắt. Gọi I là tâm của khối cầu có thể tích lớn nhất thỏa yêu cầu bài toán.
Suy ra I thuộc đoạn thẳng C'M và mặt cầu tâm I cần tìm đi qua điểm M
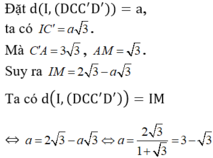
Cách khác: Chọn hệ trục tọa độ Oxyz sao cho C'(0;0;0), B' (0;3;0), D'(3;0;0), C (0;0;3).
Khi đó M(2;2;2)
Ta có phương trình đường thẳng C'M là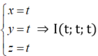 
với 2 > 0 > t do I thuộc đoạn thẳng C'M
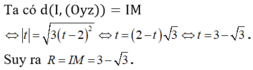
Chọn D
Ta chia khối lập phương thành hai khối lăng trụ đứng;
Ứng với mỗi khối lăng trụ đứng ta có thể chia thành ba khối tứ diện đều mà các đỉnh của tứ diện cũng là đỉnh của hình lập phương.
Vậy có tất cả là 6 khối tứ diện có thể tích bằng nhau.
Thể tích khối lập phương: \(4^3=64\left(cm^3\right)\)
Thể tích 1 khối rubik: \(2^3=8\)
Có thể chứa được: \(\dfrac{64}{8}=8\) khối rubik
