Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Hình hộp có đáy là hình vuông cạnh: 12 - 2x
Chiều cao của hình hộp là: x
Thể tích hình hộp là y = x ( 12 - 2 x ) 2
Bài toán đưa về tìm x ∈ (0; 6) để hàm số y = f ( x ) = x ( 12 - 2 x ) 2 có giá trị lớn nhất.
y ' = 1 ( 12 - 2 x ) 2 + x . 2 . ( 12 - 2 x ) . ( - 2 )
12 x 2 - 96 x + 144 ;
y' xác định ∀ x ∈ (0; 6)
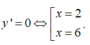
Bảng biến thiên
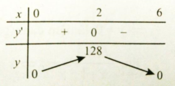
Hàm số đạt giá trị lớn nhất tại x=2

Đáp án là A
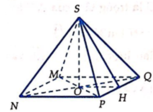
Gọi cạnh đáy, cạnh bên của hình hộp đứng lần lượt là x và y ( x ,y > 0)
Ta có:
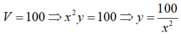
Khi đó:
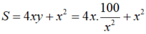
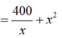
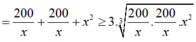
![]()
Vậy S đạt giá trị nhỏ nhất bằng 30 40 3 khi
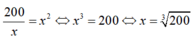

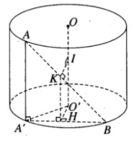
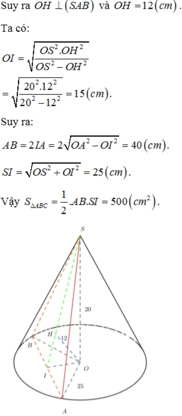
Ta có công thức S xq = 2 π rl với r = 50 cm , l = 50 cm.
Do đó S xq = 2 π .50.50 = π .5000( cm 2 ) và V = π r 2 h = 125000. π ( cm 3 )

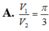

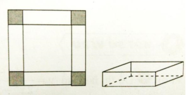

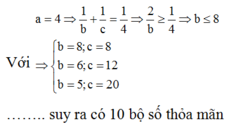


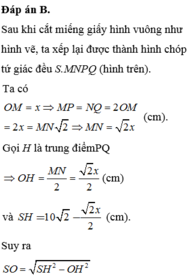
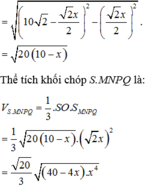
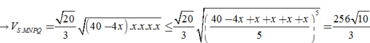
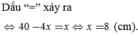
Lời giải:
Thể tích của chiếc hộp đó là:
\(V=x.x.h=500\Leftrightarrow x^2h=500\)
\(\Rightarrow h=\frac{500}{x^2}\)
Diện tích của chiếc hộp đó bao gồm diện tích một đáy và 4 mặt bao quanh:
\(S(x)=x^2+4xh\)
\(\Leftrightarrow S(x)=x^2+4x.\frac{500}{x^2}=x^2+\frac{2000}{x}\)
Đến đây có thể sử dụng đạo hàm rồi lập bảng biến thiên để tìm S(x) min, hoặc sử dụng cách ngắn gọn là:
Áp dụng BĐT Cô- si: \(x^2+\frac{2000}{x}=x^2+\frac{1000}{x}+\frac{1000}{x}\geq 3\sqrt[3]{x^2.\frac{1000}{x}.\frac{1000}{x}}=300\)
Hay \(S(x)\geq 300\)
Dấu bằng xảy ra khi \(x^2=\frac{1000}{x}\Leftrightarrow x=10\)
Đáp án B