Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chọn gốc thế năng tại mặt đất.
Cơ năng của vật tại vị trí ném: \(W_1=mgh_1+\dfrac{1}{2}mv_1^2\)
Cơ năng vật ở độ cao cực đại: \(W_2=mgh_2\)
Mà ta có: \(W_1=W_2\)
\(\Rightarrow mgh_1+\dfrac{1}{2}mv^2_1=mgh_2\) \(\Rightarrow gh_1+\dfrac{1}{2}v_1^2=gh_2\)
Với \(\left\{{}\begin{matrix}g=10\\h_1=40m\\v_1=10\end{matrix}\right.\) \(\Rightarrow h_2=45m\)
b) Ta vẫn chọn gốc thế năng tại vị trí cũ. 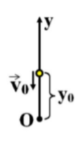
\(y=y_0+v_0t-\dfrac{1}{2}gt^2=40-10t-\dfrac{1}{2}\cdot10\cdot t^2=0\)
( vì khi vật chạm đất thì y=0) \(\Rightarrow t=2s\)
c) Thời gian vật rơi khi chạm đất: \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot40}{10}}=2\sqrt{2}s\)
Vận tốc vật khi chạm đất:
\(v=\sqrt{v^2_0+\left(gt\right)^2}=\sqrt{10^2+\left(10\cdot2\sqrt{2}\right)^2}=30\)m/s

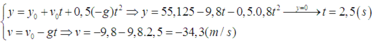

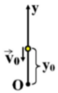
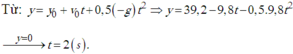
vận dụng công thức sau để giải:
∆x = (v0+v).∆t / 2
∆t là thời gian vật thực hiện độ dời ∆x với vận tốc thay đổi từ v0 đến v.
Lưu ý ở bài này giây thứ 1 tính từ thời điểm t=0 đến t=1
Giây thứ 4 tính từ thời điểm t=3 đến t=4
(**) Công thức không phụ thuộc thời gian trong chuyển động thẳng biến đổi đều :
v^2 - v0^2 = 2.a.∆x
Với a là gia tốc, vật thực hiện độ dời ∆x với vận tốc thay đổi từ v0 đến v.