Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp
Công thức tính quãng đư ờng rơi tự do: h = g t 2 2
S ư dụng công thức tính giá trị trung bình và công thức tính sai số
Cách giải:
Ta có:
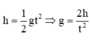
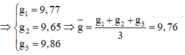
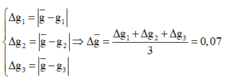
=> g = 9,76 ± 0,07 (m/s )

Chọn đáp án A
@ Lời giải:
Ban đầu lò xo giãn một đoạn Δl0, sau khoảng thời gian thả rơi lò xo và vật → lò xo co về trạng thái không biến dạng. Khi ta giữ cố định điểm chính giữa của lò xo, con lắc sẽ dao động quanh vị trí cân bằng mới.
+ Khi giữ cố định điểm chính giữa của lò xo, phần lò xo tham gia vào dao động có độ cứng k = 2k0 = 50 N/m.
→ Tần số góc của dao động
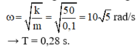
→ Độ biến dạng của lò xo tại vị trí cân bằng mới

+ Ta chú ý rằng tại thời điểm t1 vật ở vị trí có li độ x = A 2 = 2 c m → sau khoảng thời gian Δt = t2 – t1 = 0,25T = 0,07 s vật đi vị trí có li độ x = 3 2 A
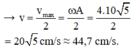

Chọn đáp án A
@ Lời giải:
Ban đầu lò xo giãn một đoạn Δ l 0 , sau khoảng thời gian thả rơi lò xo và vật → lò xo co về trạng thái không biến dạng. Khi ta giữ cố định điểm chính giữa của lò xo, con lắc sẽ dao động quanh vị trí cân bằng mới.
+ Khi giữ cố định điểm chính giữa của lò xo, phần lò xo tham gia vào dao động có độ cứng k = 2 k 0 = 50 N / m .
→ Tần số góc của dao động ω = k m = 50 0 , 1 = 10 5 rad/s → T = 0,28 s.
→ Độ biến dạng của lò xo tại vị trí cân bằng mới Δ l = m g k = 0 , 1.10 50 = 2 cm.
+ Vận tốc của con lắc tại thời điểm t 1 là v 0 = g t 1 = 10.0 , 02 15 = 0 , 2 15 m/s.
→ Biên độ dao động của con lắc A = Δ l 2 + v 0 ω 2 = 2 2 + 20 15 10 5 2 = 4 cm.
+ Ta chú ý rằng tại thời điểm t 1 vật ở vị trí có li độ x = A 2 = 2 cm → sau khoảng thời gian Δ t = t 2 – t 1 = 0 , 25 T = 0 , 07 s vật đi vị trí có li độ x = 3 2 A → v = v m a x 2 = ω A 2 = 4.10 5 2 = 20 5 cm/s ≈ 44,7 cm/s.

+ 10 dao động toàn phần và tính được kết quả t = 20 , 102 ± 0 , 269 s ⇒ T = 2 , 0102 ± 0 , 0269 s
T = 2 π l g ⇒ g = 4 π 2 l T 2 ⇒ g ¯ = 4 π 2 l ¯ T ¯ 2 = 4 π 2 .1 , 000 2 , 0102 2 ≈ 9 , 899 m/s 2
Δ g g ¯ = Δ l l ¯ + 2 Δ T T ¯ = 0 , 001 1 + 2. 0 , 0269 2 , 0102 ≈ 0 , 0277635 ⇒ Δ g = 9 , 899.0 , 0277635 ≈ 0 , 275 m/s 2
Gia tốc trọng trường do học sinh đo được tại nới làm thí nghiệm là g = 9 , 899 ± 0 , 275 m/s 2 .
Chọn đáp án C

Chọn C.
10 dao động toàn phần và tính được kết quả
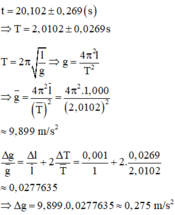
Gia tốc trọng trường do học sinh đo được tại nới làm thí nghiệm là 9 , 899 ± 0 , 275 m / s 2 .
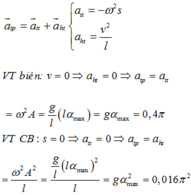
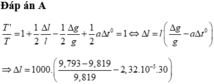



Đáp án B
Phương pháp: Công thức rơi tự do: h = gt2/2
Sử dụng công thức tính giá trị trung bình và công thức tính sai số
Cách giải:
Ta có: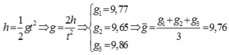
Có: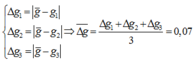
=> g = 9,76 ± 0,07 (m/s2)