Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
@ Lời giải:
Ban đầu lò xo giãn một đoạn Δl0, sau khoảng thời gian thả rơi lò xo và vật → lò xo co về trạng thái không biến dạng. Khi ta giữ cố định điểm chính giữa của lò xo, con lắc sẽ dao động quanh vị trí cân bằng mới.
+ Khi giữ cố định điểm chính giữa của lò xo, phần lò xo tham gia vào dao động có độ cứng k = 2k0 = 50 N/m.
→ Tần số góc của dao động
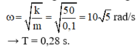
→ Độ biến dạng của lò xo tại vị trí cân bằng mới

+ Ta chú ý rằng tại thời điểm t1 vật ở vị trí có li độ x = A 2 = 2 c m → sau khoảng thời gian Δt = t2 – t1 = 0,25T = 0,07 s vật đi vị trí có li độ x = 3 2 A
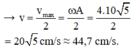

Chọn đáp án A
@ Lời giải:
Ban đầu lò xo giãn một đoạn Δ l 0 , sau khoảng thời gian thả rơi lò xo và vật → lò xo co về trạng thái không biến dạng. Khi ta giữ cố định điểm chính giữa của lò xo, con lắc sẽ dao động quanh vị trí cân bằng mới.
+ Khi giữ cố định điểm chính giữa của lò xo, phần lò xo tham gia vào dao động có độ cứng k = 2 k 0 = 50 N / m .
→ Tần số góc của dao động ω = k m = 50 0 , 1 = 10 5 rad/s → T = 0,28 s.
→ Độ biến dạng của lò xo tại vị trí cân bằng mới Δ l = m g k = 0 , 1.10 50 = 2 cm.
+ Vận tốc của con lắc tại thời điểm t 1 là v 0 = g t 1 = 10.0 , 02 15 = 0 , 2 15 m/s.
→ Biên độ dao động của con lắc A = Δ l 2 + v 0 ω 2 = 2 2 + 20 15 10 5 2 = 4 cm.
+ Ta chú ý rằng tại thời điểm t 1 vật ở vị trí có li độ x = A 2 = 2 cm → sau khoảng thời gian Δ t = t 2 – t 1 = 0 , 25 T = 0 , 07 s vật đi vị trí có li độ x = 3 2 A → v = v m a x 2 = ω A 2 = 4.10 5 2 = 20 5 cm/s ≈ 44,7 cm/s.

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

