Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mk chịu lun ! ghét toán hình ! à mk vẽ đc hình !! ai giải đc thì giải giúp bn ý nhé !!! chúc Nhật Khang làm tốt !!!

mk sợ dạng toán hình như thế này nhưng mk đc cái là vẽ đc hình ! mk vẽ hình rùi ai giúp bạn ý nha

nối AC
vì 2 tam giác MDC và ADC có chung chiều cao từ C -> AD nên tỉ lệ cạnh đáy bằng tỉ lệ diện tích
=> SADC = 2 x SMDC = 448m2
=> chiều cao kẻ từ A -> DC bằng (448 x 2) / 32 = 28
=> SABCD = \(\frac{\left(24+32\right)\times28}{2}=784\left(cm^2\right)\)
ĐS....

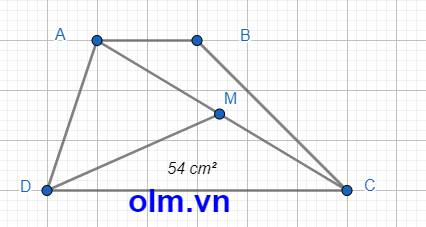
SMDC = \(\dfrac{1}{2}\)SACD (Vì hai tam giác có chung chiều cao hạ từ đỉnh D xuống đáy AC và MC = \(\dfrac{1}{2}\)AC)
⇒SACD = SMDC \(\times\) 2 = 54 \(\times\) 2 = 108 (cm2)
SABC = \(\dfrac{1}{3}\)SADC ( vì hai tam giác có chiều cao bằng chiều cao của hình thang và AB = \(\dfrac{1}{3}\)CD)
⇒SABC = 108 \(\times\) \(\dfrac{1}{3}\) = 36 (cm2)
SABCD = SABC + SACD = 36 + 108 = 144 (cm2)

\(AM=2MD\Rightarrow\dfrac{AM}{AD}=\dfrac{2}{3}\)
\(BN=\dfrac{2}{3}NC\Rightarrow\dfrac{NC}{BC}=\dfrac{3}{5}\)
Hai tg ABD và tg BCD có đường cao từ D->AB = đường cao từ B->CD nên
\(\dfrac{S_{ABD}}{S_{BCD}}=\dfrac{AB}{CD}=\dfrac{4}{5}\)
\(\Rightarrow S_{ABD}=\dfrac{4}{9}xS_{ABCD}\) và \(S_{BCD}=\dfrac{5}{9}xS_{ABCD}\)
Hai tg ABM và tg ABD có chung đường cao từ B->AD nên
\(\dfrac{S_{ABM}}{S_{ABD}}=\dfrac{AM}{AD}=\dfrac{2}{3}\Rightarrow S_{ABM}=\dfrac{2}{3}xS_{ABD}=\dfrac{2}{3}x\dfrac{4}{9}xS_{ABCD}=\dfrac{8}{27}xS_{ABCD}\)
Hai tg CND và tg BCD có chung đường cao từ D->BC nên
\(\dfrac{S_{CND}}{S_{BCD}}=\dfrac{CN}{BC}=\dfrac{3}{5}\Rightarrow S_{CND}=\dfrac{3}{5}xS_{BCD}=\dfrac{3}{5}x\dfrac{5}{9}xS_{ABCD}=\dfrac{1}{3}xS_{ABCD}\)
\(\Rightarrow\dfrac{S_{ABM}}{S_{CND}}=\dfrac{\dfrac{8}{27}xS_{ABCD}}{\dfrac{1}{3}xS_{ABCD}}=\dfrac{8}{9}\)