Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Độ nở dài của dây tải điện: Dl = a l 0 Dt = 0,414 m = 41,4 cm.

t1 = 20o C, l1 = 1800 m
t2 = 50o C
α = 11,5.10-6 (k-1)
Δl = ?
Áp dụng công thức :
Δl = αl1Δt
Δl = 11,5.10-6.1800.(50 - 20) = 0,621 m
Vậy độ nở dài của dây tải điện là Δl = 0,621 (m)

\(\Delta l=\alpha l_0\Delta t=11,5.10^{-6}.1800.\left(50-20\right)=0,612m\)

Độ tăng nhiệt độ:
\(\Delta t=t_2-t_1=50-20=30^oC\)
Độ nở dài của dây dẫn:
\(l=l_0\left(1+\alpha\Delta t\right)=1500\cdot\left(1+11,5\cdot10^{-6}\cdot30\right)=1500,5175m\)

Độ nở dài của dây tải điện đó khi nhiệt độ tăng lên đến 50 độ C là:
\(\Delta l=l-l_0=\alpha.l_0.\Delta t=11,5.10^{-6}.30.1800=0,621\left(m\right)\)Vậy: ...

Chọn đáp án B
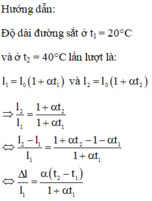
Vì α t 1 << 1 nên khi nhiệt độ tăng từ t 1 = 20 ° C đến t 2 = 40 ° C thì đoạn đường sắt này sẽ dài thêm một đoạn đường gần đúng bằng
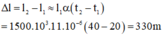

Gọi \(t_2\) là nhiệt độ để hai sợi chênh lệch nhau 0,3cm.
Độ dài sợi đồng ở \(t_2\left(^oC\right)\) là:
\(l_1=l_{01}\cdot\left(1+\alpha_1\cdot\Delta t\right)=4\cdot\left(1+17,2\cdot10^{-6}\cdot\left(t_2-10\right)\right)\)
Độ dài sợi dây sắt ở \(t_2\left(^oC\right)\) là:
\(l_2=l_{02}\left(1+\alpha_2\cdot\Delta t\right)=4\cdot\left(1+11,4\cdot10^{-6}\cdot\left(t_2-10\right)\right)\)
Để chúng lệch nhau \(0,3cm=0,003m\).
\(\Rightarrow\Delta l=l_1-l_2\)
\(\Rightarrow\Delta l=4\cdot\left(1+17,2\cdot10^{-6}\cdot\left(t_2-10\right)\right)-4\cdot\left(1+11,4\cdot10^{-6}\cdot\left(t_2-10\right)\right)=0,003\)
\(\Rightarrow t_2=139,31^oC\)

Đáp án: D
Gọi l1 là chiều dài của thanh đồng thau, l2 là chiều dài của thanh thép.
Theo giả thiết, ở nhiệt độ bất kỳ ta đều có:
l2 – l1 = 2 cm (1)
Ở 0 oC ta cũng có:
l02 – l01 = 2 cm (2)
Mặt khác, ta lại có:
l2 = l02(1 + α2∆t) và l1 = l01(1 + α1∆t)
Thay l1, l2 vào (1) ta được:
l02(1 + α2∆t) - l01(1 + α1∆t) = l02 – l01
→ l02.α2 = l01.α1 (3)
Từ (2) và (3), chú ý rằng :
α2 = 18.10-6 K-1 và α1 = 11.10-6 K-1
Ta suy ra được chiều dài của thanh thép và thanh đồng ở 0 oC là 5,1cm và 3,1cm
Đáp án: A
Độ nở dài của dây tải điện:
Dl = al0Dto = 0,414 m = 41,4 cm.