Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(x\) là vận tốc của thuyền so với bờ
Ta có :
\(\dfrac{AB}{x+3}+\dfrac{AB}{x-3}=1\left(h\right)\)
\(\Leftrightarrow\dfrac{4}{x+3}+\dfrac{4}{x-3}=1\)
\(\Leftrightarrow x=6km\backslash h\)

Chọn D
+ Gọi v 13 là vận tốc của thuyền với bờ
v 23 là vận tốc của nước với bờ bằng
v 12 là vận tốc của thuyền so với dòng nước
+ Khi xuôi dòng: v 13 = v 12 + v 23
+ Khi ngược dòng: v 13 = v 12 - v 23 ⇒ v 13 - v 13 = 2 v 23
⇔ S 2 , 5 - S 3 = 2 . v 23 ⇒ v 23 = 1 2 ( S 2 , 5 - S 3 ) ⇒ t c = S v 23 = 30 h

\(t_x+t_{ng}=1h\)
\(AB=4km\)
\(v_{nb}=3km/h\)
\(v_{tn}=?\)
GIẢI :
Thời gian thuyền xuôi dòng :
\(t_x=\frac{AB}{v_{tn}+v_{nb}}=\frac{4}{v_{tn}+3}\) (1)
thời gian thuyền ngược dòng :
\(t_{ng}=\frac{AB}{v_{tn}-v_{nb}}=\frac{4}{v_{tn}-3}\)(2)
lại có: \(t_x+t_1=1\)
từ (1) và (2) => \(\frac{4}{v_{tn}+3}+\frac{4}{v_{tn}-3}=1\)
=> \(v_{tn}=9m/s\)
Vậy vận tốc của thuyền so với mặt nước là 9m/s

vận tốc thuyền so với bờ
\(v_{13}=v_{12}+v_{23}=15+3=18\left(\dfrac{km}{h}\right)\)
thời gian chuyển động của thuyền là
\(t=\dfrac{s}{v}=\dfrac{18}{18}=1\left(h\right)\)
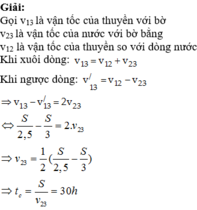

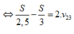


thời gian thuyền xuôi dòng là
tx=\(\dfrac{AB}{v_{t,n}+v_{n,b}}\)
thời gian thuyền đi ngược dòng là
tn=\(\dfrac{AB}{v_{t,n}-v_{n,b}}\)
vì thuyền đi từ A-B rồi quay lại A mất 1h
tn+tx=1\(\Rightarrow\)vt,n=9km/h