Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B

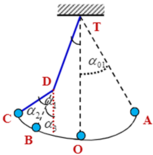
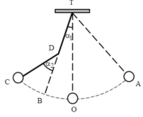
Xét trong nửa chu kì, khi vật đi từ A → C, ta có thể chia chuyển động của vật thành các giai đoạn sau:
Giai đoạn 1: Chuyển động từ A đến B tương tự như dao động của con lắc đơn với chiều dài TA = 1,92 m
+ Chu kì dao động của con lắc trong trường hợp này T 1 = 2 π TA g = 2 π 1 , 92 π 2 ≈ 2 , 77
Biên độ góc của con lắc trong dao động này là α o
Giai đoạn 2: Chuyển động từ B đến C tương tự như dao động của con lắc đơn với chiều dài DC = 0,64 m
+ Chu kì dao động của con lắc trong trường hợp này T 2 = 2 π DC g = 2 π 0 , 64 π 2 = 1 , 6
Dễ thấy rằng biên độ dao động của con lắc trong trường hợp này là α′0 = 2.40 = 80.
Quá trình vướng đinh không làm thay đổi cơ năng của con lắc do vậy độ cao của con lắc tại A và C là như nhau.
→ TO(1 – cosα0) = TO – TDcosα1 – DCco2α1.
Thay các giá trị đã biết vào biểu thức, ta tìm được α0 ≈ 5,70.
→ Thời gian để con lắc chuyển động từ A đến B là
t 1 = 180 0 − arcos 4 0 5 , 7 0 360 0 T 1 = 1 , 035
Thời gian để con lắc chuyển động từ B đến C ứng với từ vị trí có li độ bằng một nửa biên độ đến vị trí biên t 2 = T 2 6 = 1 , 6 6 = 0 , 267
→ Chu kì dao động của con lắc T = 2(t1 + t2) = 2,6 s

Đáp án B
![]()
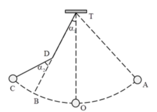
Sau khi vướng đinh:
Ta có
![]()
Động năng của con lắc ngay trước và ngay sau khi vướng đinh là bằng nhau, nên:
![]()
![]()
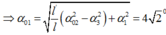
![]()
Trong 1 chu kì
Thời gian con lắc l chuyển động:
![]()
Thời gian con lắc l /3 chuyển động: Do nên
tBC = tCB = T 2 6
Chu kì dao động của con lắc là
![]()

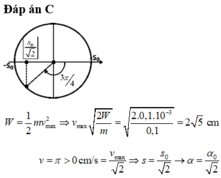
Đáp án A
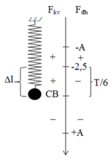
Ta có ∆l = mg/k = 0,025 m = 2,5 cm.
![]()
![]()
![]()
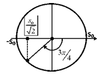
→ quãng thời gian ![]() ngược chiều nhau là T/6 →
ngược chiều nhau là T/6 →
 vật
vật
đi từ vị trí π/2 đến 2π/3 và -2π/3 đến –π/2.
→ -A/2 = 2,5 cm.
→ A = 5 cm.

Đáp án B
+ Chu kì của con lắc vướng đinh T = π l 0 g + π 0 , 5 l 0 g = 2 , 4
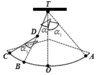

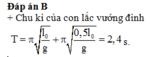
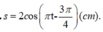
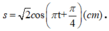
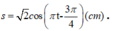
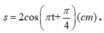
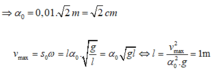
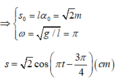

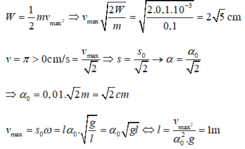
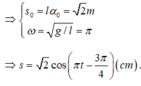
(Giá trị thời gian đặc biệt và khá quen thuộc ở các dạng toán trước).
Chú ý: Chọn chiều dương là chiều từ trái sáng phải. Đi theo chiều OA là chiều dương, đi theo chiều OC là chiều âm. Máy tính để ở chế độ rad.