Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

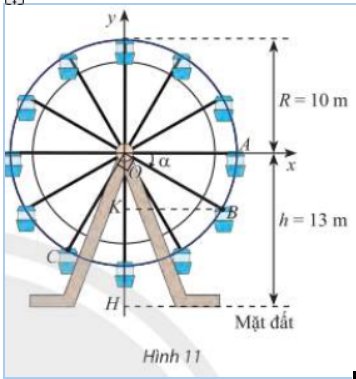
Thanh OM quay được \(3\dfrac{1}{10}\) vòng thì \(\alpha=3\dfrac{1}{10}\cdot360^o=1116^o\)
Từ M kẻ MH \(\perp\) Ox
\(\Rightarrow OH=15\cdot\left|cos1116^o\right|\approx12,1\)
Vậy độ dài bóng O'M' của OM khi thanh quay được \(3\dfrac{1}{10}\) là 12,1cm.

a) Khi kim phút quay theo ngược chiều kim đồng hồ để nó chỉ đúng số 12, kim phút quay:
\(\frac{2}{{12}} = \frac{1}{6}\) phần của vòng tròn
b) Khi kim phút quay theo đúng chiều kim đồng hồ để nó chỉ đúng số 12, kim phút quay:
\(\frac{{10}}{{12}} = \frac{5}{6}\) phần của vòng tròn
c) Có 2 cách quay kim phút theo một chiều xác định để kim phút từ vị trí chỉ đúng số 2 về vị trí chỉ đúng số 12, đó là: ngược chiều kim đồng hồ và cùng chiều kim đồng hồ

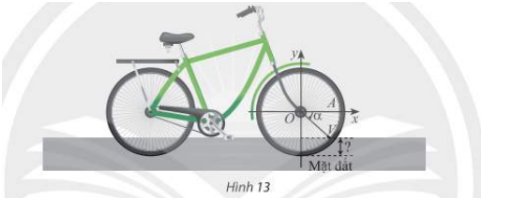
Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: \(\alpha=11\cdot60=660\left(rad\right)\)
Khi đó tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là: \(V\left(58\cdot cos\alpha,58\cdot sin\alpha\right)\approx\left(56;15,2\right)\)
Từ đó, khoảng cách từ van đến mặt đất khoảng \(58-15,2\approx42,8\left(cm\right)\)

Trong 3s, quạt quay được: \(3\cdot\dfrac{45}{60}=\dfrac{9}{4}\left(vòng\right)\)
Vậy quạt quay được 1 góc: \(2\pi\cdot\dfrac{9}{4}=\dfrac{9\pi}{2}\left(rad\right)\)
Trong 3 giây quay được:
3*45/60=9/4(vòng)
Số đo góc quay được:
2pi*9/4=9/2*pi

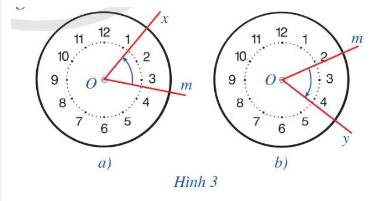
a) Chiều quay từ tia Om đến tia Ox trong Hình 3a là chiều quay ngược chiều kim đồng hồ
b) Chiều quay từ tia Om đến tia Oy trong Hình 3b là chiều quay cùng chiều kim đồng hồ.

Xác suất: \(P=\dfrac{6}{36}.\dfrac{24}{36}=\dfrac{1}{9}\) (con số 24 ở đây là từ 13 tới 36 có 24 số)