K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 6 2021
do tam giác ABC có góc A=90\(^o\)=>\(\Delta ABC\) vuông tại A
\(\Delta ABH\sim\Delta CBA\left(g.g\right)\)( vì góc B chung, góc AHB=góc BAC)
\(=>\dfrac{AB}{BC}=\dfrac{BH}{BA}=>AB^2=BH.BC\)(1)
b,dựa vào (1)\(=>AB=\sqrt{BH.BC}=\sqrt{BH\left(BH+HC\right)}=\sqrt{4.\left(4+9\right)}=2\sqrt{13}cm\)
theo pytago\(=>AC=\sqrt{BC^2-AB^2}=\sqrt{13^2-\left(2\sqrt{13}\right)^2}=3\sqrt{13}cm\)
c,theo tính chất phan giác=>\(\dfrac{AB}{BC}=\dfrac{AD}{DC}=>\dfrac{AD}{DC}=\dfrac{2}{3}\)\(=>DC=\dfrac{3}{2}AD\)
có: \(AD+DC=AC=>AD+\dfrac{3}{2}AD=3\sqrt{13}=>AD=\dfrac{6\sqrt{13}}{5}cm\)
\(=>S\left(\Delta DBA\right)=\dfrac{AB.AD}{2}=15,6cm^2\)
có: tam giac BDA đồng dạng tam giác BEH(g.g)(do góc B1=góc B2, góc A=góc H=90 độ)
=>góc E2= góc D1
mà góc E2=góc E1(đối đỉnh)=>góc D1=góc E1=>tam giác AED cân tại A
=>AE=AD=\(\dfrac{6\sqrt{13}}{5}cm\),
theo pytago=>AH=\(\sqrt{AB^2-BH^2}=\sqrt{ \left(2\sqrt{13}\right)^2-4^2}=6cm\)
=>EH=AH-AE=\(6-\dfrac{6\sqrt{13}}{5}cm\)
=>\(S\left(\Delta EBH\right)=\dfrac{1}{2}BH.EH\) rồi tự tính ra rồi lập tỉ số 2 S tam giác (mỏi tay)
DX
17 tháng 12 2022
11)\(\dfrac{3x+1}{x-5}+\dfrac{2x}{x-5}=\dfrac{3x+2x+1}{x-5}=\dfrac{5x+1}{x-5}\)
12)\(\dfrac{4-x^2}{x-3}+\dfrac{2}{x^2-9}=\dfrac{4-x^2}{x-3}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{\left(4-x^2\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{2+\left(2-x\right)\left(2+x\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\)
13)
\(\dfrac{3}{4x-2}+\dfrac{2x}{4x^2-1}=\dfrac{3}{2\left(2x-1\right)}+\dfrac{2x}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{3\left(2x+1\right)}{2\left(2x-1\right)\left(2x+1\right)}+\dfrac{2.2x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{6x+3+4x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{10x+3}{2\left(2x-1\right)\left(2x+1\right)}\)
14)
\(\dfrac{2x+1}{2x-4}+\dfrac{5}{x^2-4}=\dfrac{2x+1}{2\left(x-2\right)}+\dfrac{5}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(2x+1\right)\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\dfrac{5.2}{2\left(x-2\right)\left(x+2\right)}=\dfrac{2x^2+5x+12}{2\left(x-2\right)\left(x+2\right)}\)
AB
0
19 tháng 11 2023
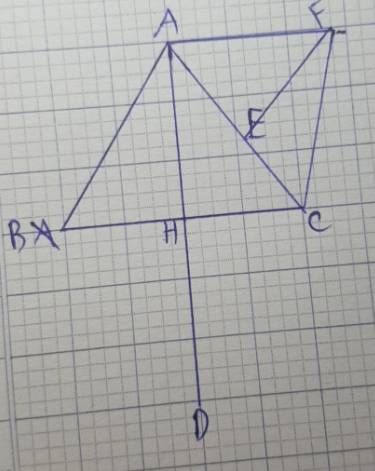
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)
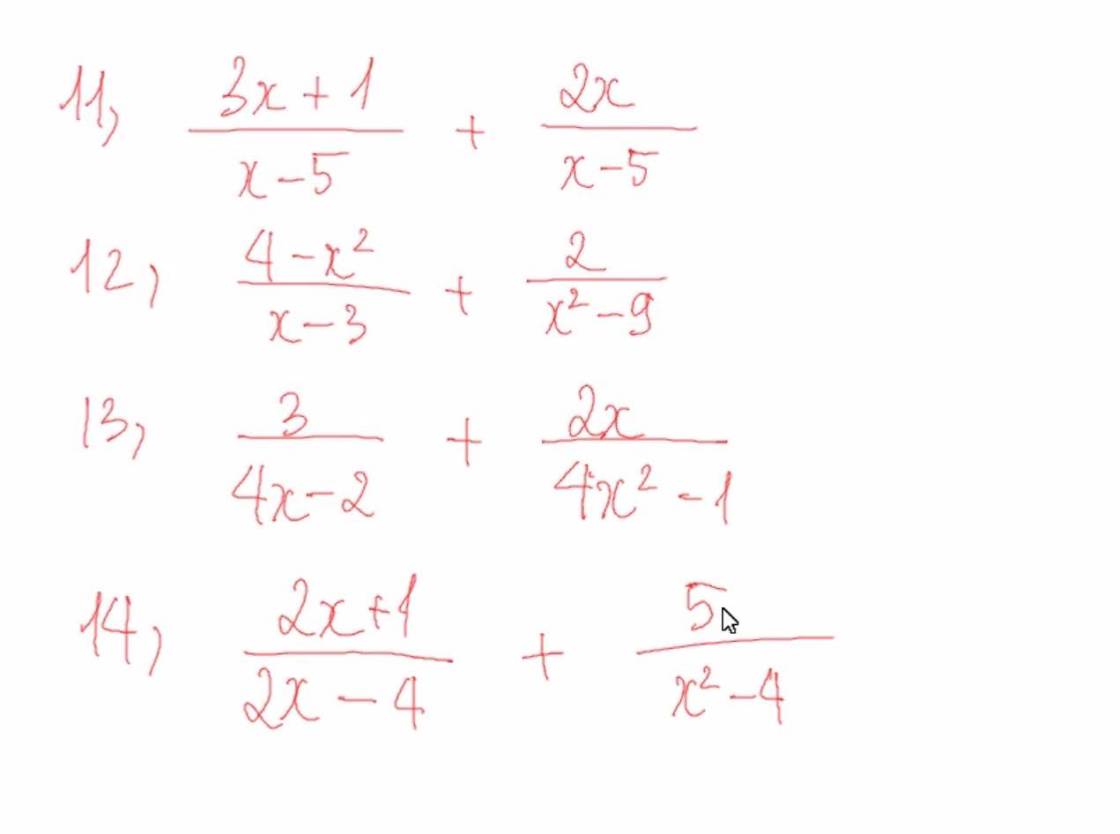
\(a)7x-21=0.\\ \Leftrightarrow x=3.\)
\(b)3x-5=2x+7.\\ \Leftrightarrow x=12.\)
\(c)6x+18=0.\\ \Leftrightarrow x=-3.\\ d)5x+2=4x-1.\\ \Leftrightarrow x=-3.\)
Bài 1:
a: 7x-21=0
=>7x=21
hay x=3
b: 3x-5=2x+7
=>3x-2x=7+5
=>x=12
c: 6x+18=0
=>6x=-18
hay x=-3
d: 5x+2=4x-1
=>5x-4x=-1-2
=>x=-3