Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

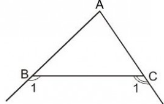
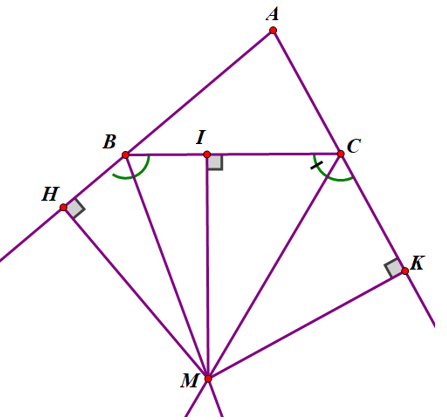
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).

bn tự vẽ hình nha
ta có a+b+c=180(tổng 3 góc của tg) suy ra a+80+30=180 suy ra a=180-110=70 độ
ta có BAD=CAD=BAC/2(tia phân giác ad)
suy ra bad=cad=70/2=35 độ
ta có ADC=BAD+ABD=35+80=115(độ)
suy ra ADB=180-115=65 ĐỘ
CHỖ NÀO KO HIỂU THÌ HỎI MÌNH NHA BN HI HI
CHÚC BN HỌC TỐT

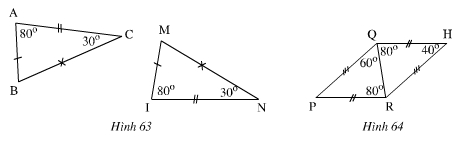
Hình 63
Ta có:
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
Hình 64 :
ΔPQR có:
Và QH = RP, HR = PQ, QR ( cạnh chung )
Nên ΔHQR = ΔPRQ
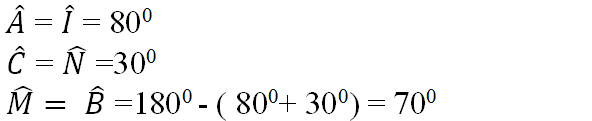
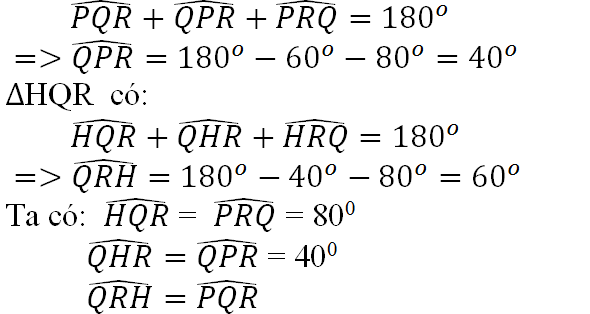
Bạn ghi rõ đề đi bạn