Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(BC\) \(\subset\)\(\left(SBC\right)\)
Tìm giao tuyến của của \(\left(OMN\right)\)và \(\left(SBC\right)\):
\(N\)là điểm chung thứ nhất
Ta có : \(MO\)\(\subset\)\(\left(AMO\right)\)\(\equiv\)\(\left(SAH\right)\)với \(H=AO\)\(\cap\) \(BC\)
\(\left(SAH\right)\)\(\cap\) \(\left(SBC\right)\)= \(SH\)
Trong \(\left(SAH\right)\): \(MO\)\(\cap\) \(SH\)= \(K\)
\(K\)là điểm chung thứ 2.
Vậy \(\left(OMN\right)\)\(\cap\)\(\left(SBC\right)\)= \(NK\)
Trong \(\left(SBC\right):\)\(NK\)\(\cap\)\(BC\)= \(P\)
Vậy \(\left(OMN\right)\)\(\cap\) \(BC\)= \(P\)
Ta có N thuộc (OMN)
C thuộc đường thẳng BC
Mà N trùng với C => N là giao điểm của (OMN) và BC

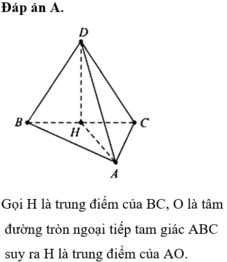
Đáp án A
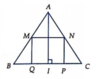
Gọi cạnh hình vuông là x. Ta có ![]()
![]()
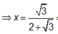
![]()
Gọi V 1 là thể tích hình nón khi quay tam giác ABC quanh trục trung tuyến AI , V 2 là thể tích hình trụ khi quay hình vuông MNPQ quanh trục AI thì
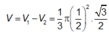
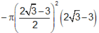

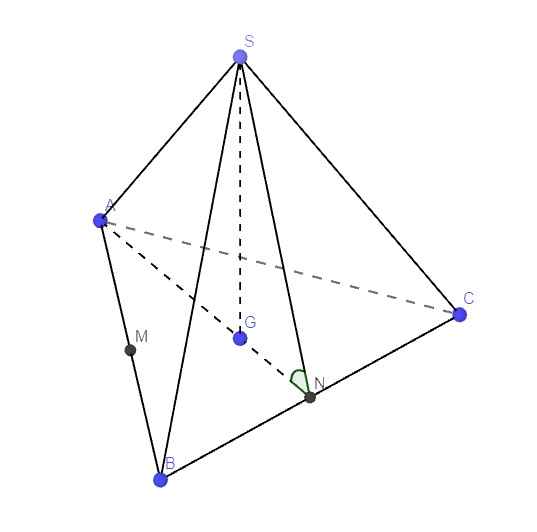
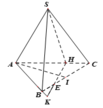
Gọi G là trọng tâm ABC \(\Rightarrow SG\perp\left(ABC\right)\) do S.ABC là chóp đều
\(\Rightarrow SG\perp BC\)
Mà \(AN\perp BC\) (do tam giác ABC đều)
\(\Rightarrow BC\perp\left(SAN\right)\)
\(\Rightarrow\widehat{SNA}\) là góc giữa (ABC) và (SBC)
\(AN=\dfrac{AB.\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
\(AG=\dfrac{2}{3}AN=\dfrac{2a\sqrt{3}}{3}\) ; \(GN=\dfrac{1}{3}AN=\dfrac{a\sqrt{3}}{3}\) (t/c trọng tâm)
\(SG=\sqrt{SA^2-AG^2}=a\)
\(\Rightarrow tan\widehat{SNA}=\dfrac{SG}{GN}=\sqrt{3}\Rightarrow\widehat{SNA}=60^0\)


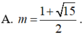
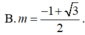
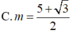
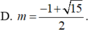

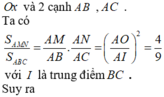
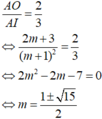
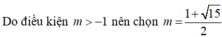
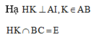
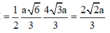

\(\dfrac{S_{ABC}}{S_{AMN}}=\dfrac{\dfrac{1}{2}AB.AC.sinA}{\dfrac{1}{2}AM.AN.sinA}=\dfrac{AB.AC}{\dfrac{1}{2}AB.\dfrac{2}{3}AC}=3\)
Dạ em cảm ơn nhiều ạ!!!