Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Góc giữa cạnh SA và đáy là S A F ^ ,
Vì tam giác ABC và SBC là tam giác đều cạnh a nên ta có
![]()
Vậy ![]()

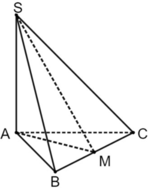
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Mà \(\left\{{}\begin{matrix}BC=\left(SBC\right)\cap\left(ABC\right)\\SB=\left(SAB\right)\cap\left(SBC\right)\\AB=\left(SAB\right)\cap\left(ABC\right)\end{matrix}\right.\) \(\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABC)
\(\Rightarrow\widehat{SBA}=60^0\Rightarrow SA=AB.tan60^0=a\sqrt{3}\)
\(SA\perp\left(ABC\right)\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{SCA}\approx40^053'\)
Gọi M là trung điểm SB \(\Rightarrow GM=\dfrac{1}{3}AM\) (tính chất trọng tâm)
\(\Rightarrow d\left(G;\left(SBC\right)\right)=\dfrac{1}{3}d\left(A;\left(SBC\right)\right)\)
Từ A kẻ \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}=\dfrac{1}{3a^2}+\dfrac{1}{a^2}=\dfrac{4}{3a^2}\Rightarrow AH=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow d\left(G;\left(SBC\right)\right)=\dfrac{1}{3}AH=\dfrac{a\sqrt{3}}{6}\)

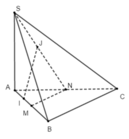
+ Ta có S A B ⊥ A B C S A C ⊥ A B C S A C ∩ S A B = S A ⇒ S A ⊥ A B C
+ Xác định điểm N, mặt phẳng qua SM và song song với BC cắt AC tại N ⇒ N là trung điểm của AC (MN//BC).
+ Xác định được góc giữa hai mặt phẳng (SBC) và (ABC) là S B A ^ = 60 °
⇒ SA = AB.tan 60 ° = 2a 3
AC = A B 2 + B C 2 = 2 a 2
+ Gọi IJ là đoạn vuông góc chung của AB và SN (điểm I thuộc AB và điểm J thuộc SN). Vậy khoảng cách giữa AB và SN là IJ. Ta sẽ biểu thị IJ → qua ba vectơ không cùng phương A B → ; A C → ; A S → .
I J → = I A → + A N → + N J → = m A B → + 1 2 A C → + p N S → = m A B → + 1 2 A C → + p N A → + A S → = m A B → + 1 − p 2 A C → + p A S →
Ta có: I J → ⊥ A B → I J → ⊥ N S → ⇔ I J → . A B → = 0 I J → . N S → = 0
Thay vào ta tính được m = -6/13; p = 1/13
Do đó: I J → = − 6 13 A B → + 6 13 A C → + 1 13 A S → . Suy ra
169 I J 2 = 36 A C 2 + 36 A B 2 + A S 2 − 72 A B → . A C → .
Thay số vào ta tính được IJ = 2 a 39 13 .
Vậy d(AB; SN) = 2 a 39 13 .
Đáp án D

tam giác ABC đều nên AM ⊥ BC ⇒ SM ⊥ BC (theo định lí ba đường vuông góc)
Đáp án B

Nhận xét
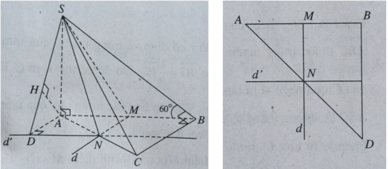
Gọi (α) là mặt phẳng qua SM và song song với AB.
Ta có BC // (α) và (ABC) là mặt phẳng chứa BC nên (ABC) sẽ cắt (α) theo giao tuyến d đi qua M và song song với BC, d cắt AC tại N.
Ta có (α) chính là mặt phẳng (SMN). Vì M là trung điểm AB nên N là trung điểm AC.
+ Xác định khoảng cách.
Qua N kẻ đường thẳng d’ song song với AB.
Gọi (P) là mặt phẳng đi qua SN và d’.
Ta có: AB // (P).
Khi đó: d(AB, SN) = d(A, (P)).
Dựng AD ⊥ d’, ta có AB // (SDN). Kẻ AH vuông góc với SD, ta có AH ⊥ (SDN) nên:
d(AB, SN) = d(A, (SND)) = AH.
Trong tam giác SAD, ta có 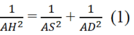
Trong tam giác SAB, ta có S A = A B . tan 60 o = 2 a 3 và AD = MN = BC/2 = a.
Thế vào (1), ta được
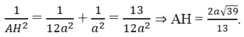

a: SO vuông góc (ABC)
=>(SGO) vuông góc (ABC)
b: ((SAB);(ABC))=(SG;AG)=góc SGA
\(AG=\dfrac{a\sqrt{3}}{3}\)
cos SGA=AG/SA=căn 3/3:2=căn 3/6
=>góc SGA=73 độ
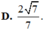
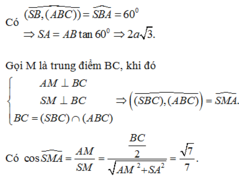
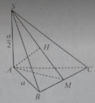
Gọi G là trọng tâm ABC \(\Rightarrow SG\perp\left(ABC\right)\) do S.ABC là chóp đều
\(\Rightarrow SG\perp BC\)
Mà \(AN\perp BC\) (do tam giác ABC đều)
\(\Rightarrow BC\perp\left(SAN\right)\)
\(\Rightarrow\widehat{SNA}\) là góc giữa (ABC) và (SBC)
\(AN=\dfrac{AB.\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
\(AG=\dfrac{2}{3}AN=\dfrac{2a\sqrt{3}}{3}\) ; \(GN=\dfrac{1}{3}AN=\dfrac{a\sqrt{3}}{3}\) (t/c trọng tâm)
\(SG=\sqrt{SA^2-AG^2}=a\)
\(\Rightarrow tan\widehat{SNA}=\dfrac{SG}{GN}=\sqrt{3}\Rightarrow\widehat{SNA}=60^0\)