
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


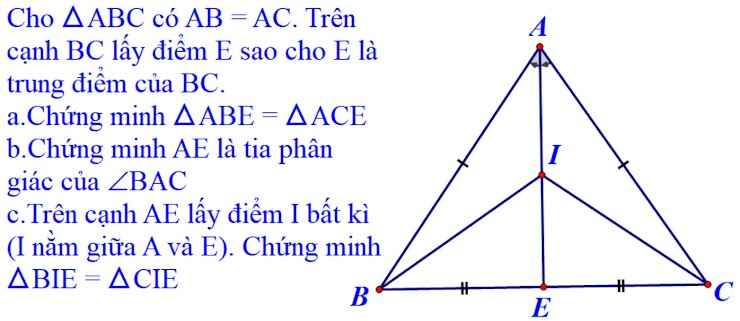
a) Xét tam giác ABE và tam giác ACE có:
+ AE chung.
+ AB = AC (gt).
+ BE = CE (E là trung điểm của BC).
=> Tam giác ABE = Tam giác ACE (c - c - c).
b) Xét tam giác ABC có: AB = AC (gt).
=> Tam giác ABC cân tại A.
Mà AE là đường trung tuyến (E là trung điểm của BC).
=> AE là phân giác ^BAC (Tính chất các đường trong tam giác cân).
c) Xét tam giác ABC cân tại A có:
AE là phân giác ^BAC (cmt).
=> AE là đường cao (Tính chất các đường trong tam giác cân).
=> AE \(\perp\) BC.
Xét tam giác BIE và tam giác CIE:
+ IE chung.
+ BE = CE (E là trung điểm của BC).
+ ^BEI = ^CEI ( = 90o).
=> Tam giác BIE = Tam giác CIE (c - g - c).

a) \(\Rightarrow\left(x-3\right)\left(x+4\right)=5.12\)
\(\Rightarrow x^2+x-72=0\)
\(\Rightarrow\left(x-8\right)\left(x+9\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-9\end{matrix}\right.\)
b) \(\Rightarrow\left(x+3\right)^2=36\)
\(\Rightarrow\left[{}\begin{matrix}x+3=6\\x+3=-6\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-9\end{matrix}\right.\)
c) \(\Rightarrow2x^2=8\Rightarrow x^2=4\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)






Bạn ơi chứng minh nhỏ hơn hoặc bằng 0 nhé
\(=-y^{2018}-\left(x^2-x+1\right)\)
\(=-y^{2018}-\left(x+1\right)^2\)
Vì \(\hept{\begin{cases}-y^{2018}\le0;\forall x,y\\-\left(x+1\right)^2\le0;\forall x,y\end{cases}}\)
\(\Rightarrow-y^{2018}-\left(x+1\right)^2\le0;\forall x,y\left(đpcm\right)\)

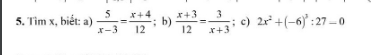



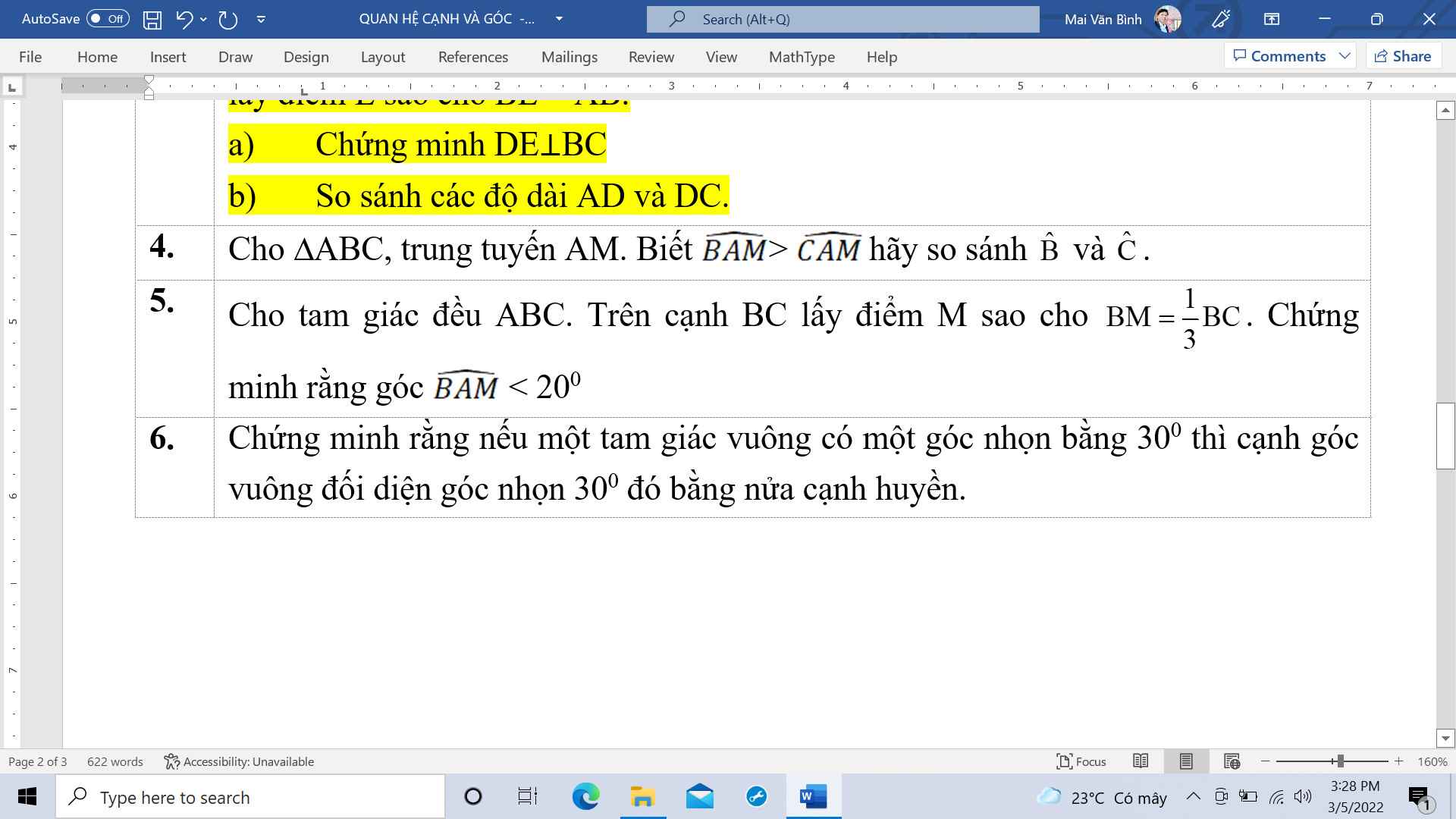
 mọi người giúp mik với ạ mik đang cần gấp ( nếu xong trg 45 phút thì càng tốt ) cảm ơn mọi người :'))
mọi người giúp mik với ạ mik đang cần gấp ( nếu xong trg 45 phút thì càng tốt ) cảm ơn mọi người :'))
a) Do M là trung điểm của BC (gt)
\(\Rightarrow MB=MC\)
Xét \(\Delta AMB\) và \(\Delta DMC\) có:
\(MB=MC\left(cmt\right)\)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
\(MA=MD\left(gt\right)\)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c-g-c\right)\)
b) Do N là trung điểm của AC (gt)
\(\Rightarrow NA=NC\)
Xét \(\Delta ANB\) và \(\Delta CNE\) có:
\(NA=NC\left(cmt\right)\)
\(\widehat{ANB}=\widehat{CNE}\) (đối đỉnh)
\(NB=NE\left(gt\right)\)
\(\Rightarrow\Delta ANB=\Delta CNE\left(c-g-c\right)\)
\(\Rightarrow\widehat{ABN}=\widehat{CEN}\) (hai góc tương ứng)
Mà \(\widehat{ABN}\) và \(\widehat{CEN}\) là hai góc so le trong
\(\Rightarrow AB\) // \(CE\)
c) Do \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{CDM}\) (hai góc tương ứng)
Mà \(\widehat{BAM}\) và \(\widehat{CDM}\) là hai góc so le trong
\(\Rightarrow AB\) // \(CD\)
Mà \(AB\) // \(CE\left(cmt\right)\)
Theo tiên đề Ơclit \(\Rightarrow E,C,D\) thẳng hàng