K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DM
1
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$
AH
Akai Haruma
Giáo viên
27 tháng 8 2023
Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k$
$\Rightarrow a=bk, c=dk$. Khi đó:
$\frac{a-b}{b}=\frac{bk-b}{b}=\frac{b(k-1)}{b}=k-1(1)$
$\frac{c-d}{d}=\frac{dk-d}{d}=\frac{d(k-1)}{d}=k-1(2)$
Từ $(1); (2)\Rightarrow \frac{a-b}{b}=\frac{c-d}{d}$
-------------------
$\frac{2a+3b}{2a-3b}=\frac{2bk+3b}{2bk-3b}=\frac{b(2k+3)}{b(2k-3)}=\frac{2k+3}{2k-3}(3)$
$\frac{2c+3d}{2c-3d}=\frac{2dk+3d}{2dk-3d}=\frac{d(2k+3)}{d(2k-3)}=\frac{2k+3}{2k-3}(4)$
Từ $(3); (4)\Rightarrow \frac{2a+3b}{2a-3b}=\frac{2c+3d}{2c-3d}$
6 tháng 7 2021
Bài 7:
a) Ta có: x:2=y:5
nên \(\dfrac{x}{2}=\dfrac{y}{5}\)
mà x+y=21
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{21}{7}=3\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=3\\\dfrac{y}{5}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=15\end{matrix}\right.\)
c) Ta có: x:2=y:7
nên \(\dfrac{x}{2}=\dfrac{y}{7}\)
mà x+y=18
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{7}=\dfrac{x+y}{2+7}=\dfrac{18}{9}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=2\\\dfrac{y}{7}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=14\end{matrix}\right.\)
Bài 8:
a) Ta có: \(\dfrac{a}{3}=\dfrac{b}{8}=\dfrac{c}{5}\)
nên \(\dfrac{2a}{6}=\dfrac{3b}{24}=\dfrac{c}{5}\)
mà 2a+3b-c=50
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2a}{6}=\dfrac{3b}{24}=\dfrac{c}{5}=\dfrac{2a+3b-c}{6+24-5}=\dfrac{50}{25}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{a}{3}=2\\\dfrac{b}{8}=2\\\dfrac{c}{5}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=16\\c=10\end{matrix}\right.\)
6 tháng 7 2021
Bài 8:
b) Ta có: \(\dfrac{x}{10}=\dfrac{y}{5}\)
nên \(\dfrac{x}{20}=\dfrac{y}{10}\)(1)
Ta có: \(\dfrac{y}{2}=\dfrac{z}{3}\)
nên \(\dfrac{y}{10}=\dfrac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{15}\)
\(\Leftrightarrow\dfrac{2x}{40}=\dfrac{3y}{30}=\dfrac{4z}{60}\)
mà 2x-3y+4z=330
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{40}=\dfrac{3y}{30}=\dfrac{4z}{60}=\dfrac{2x-3y+4z}{40-30+60}=\dfrac{330}{70}=\dfrac{33}{7}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{20}=\dfrac{33}{7}\\\dfrac{y}{10}=\dfrac{33}{7}\\\dfrac{z}{15}=\dfrac{33}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{660}{7}\\y=\dfrac{330}{7}\\z=\dfrac{495}{7}\end{matrix}\right.\)
c) Ta có: 3x=2y
nên \(\dfrac{x}{2}=\dfrac{y}{3}\)
hay \(\dfrac{x}{10}=\dfrac{y}{15}\)(1)
Ta có: 7x=5z
nên \(\dfrac{x}{5}=\dfrac{z}{7}\)
hay \(\dfrac{x}{10}=\dfrac{z}{14}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{14}\)
mà x-y+z=32
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{14}=\dfrac{x-y+z}{10-15+14}=\dfrac{32}{9}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{10}=\dfrac{32}{9}\\\dfrac{y}{15}=\dfrac{32}{9}\\\dfrac{z}{14}=\dfrac{32}{9}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{320}{9}\\y=\dfrac{480}{9}=\dfrac{160}{3}\\z=\dfrac{448}{9}\end{matrix}\right.\)
MT
2
KV
2 tháng 5 2023
Bài 6
a) (3x² + 5) + [(2x² - 5x) - (5x² + 4)]
= 3x² + 5 + (2x² - 5x - 5x² - 4)
= 3x² + 5 + 2x² - 5x - 5x² - 4
= (3x² + 2x² - 5x²) - 5x + (5 - 4)
= -5x + 1
---------‐----------
b) (x + 2)(x² - 2x + 4)
= x.x² - x.2x + x.4 + 2.x² - 2.2x + 2.4
= x³ - 2x² + 4x + 2x² - 4x + 8
= x³ + (-2x² + 2x²) + (4x - 4x) + 8
= x³ + 8
-------------------
c) (4x³ - 8x² + 13x - 5) : (2x - 1)
= (4x³ - 2x² - 6x² + 3x + 10x - 5) : (2x - 1)
= [(4x³ - 2x²) - (6x² - 3x) + (10x - 5)] : (2x - 1)
= [2x²(2x - 1) - 3x(2x - 1) + 5(2x - 1)] : (2x - 1)
= (2x - 1)(2x² - 3x + 5) : (2x - 1)
= 2x² - 3x + 5
TP
1
24 tháng 8 2023
6:
Số tiền phải trả góp là:
350000*24=8400000(đồng)
Số tiền mua chiếc TV là:
8400000:60%=14000000(đồng)
CC
3
20 tháng 7 2021
a, Ta có
\(\left|x-1,7\right|=2,3\\ \Rightarrow\left[{}\begin{matrix}x-1,7=2.3\\x-1.7=-2,3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=4\\x=-0,6\end{matrix}\right.\)
Vậy....
b, Ta có :
\(\left|x+\dfrac{3}{4}\right|-\dfrac{1}{3}=0\\ \Rightarrow\left|x+\dfrac{3}{4}\right|=\dfrac{1}{3}\\ \Rightarrow\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{3}\\x+\dfrac{3}{4}=-\dfrac{1}{3}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{5}{12}\\x=-\dfrac{13}{12}\end{matrix}\right.\)
Vậy...
KV
29 tháng 10 2023
10³ + 2¹⁵
= 1000 + 32768
= 33768
Mà 33768 : 33 = 1023 (dư 9)
Em xem lại đề
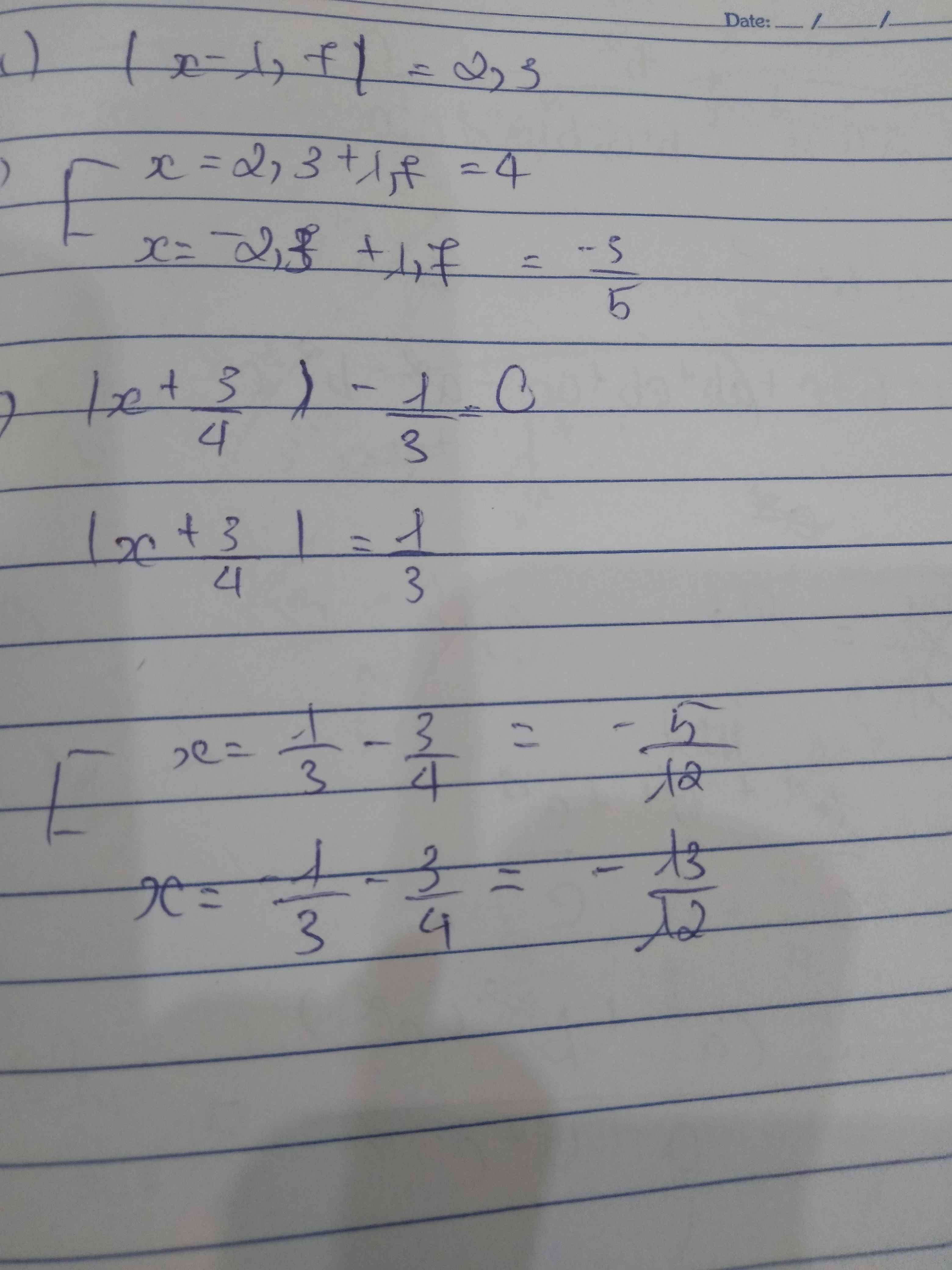
c, (4 + 1\(\dfrac{3}{5}\)) . 2\(\dfrac{1}{7}\) - 4\(\dfrac{2}{3}\): \(\dfrac{5}{9}\)
= (4 + \(\dfrac{8}{5}\)) . \(\dfrac{15}{7}\) - \(\dfrac{14}{3}\): \(\dfrac{5}{9}\)
= \(\dfrac{28}{5}\). \(\dfrac{15}{7}\) - \(\dfrac{42}{5}\)
= 12 - \(\dfrac{42}{5}\)
= \(\dfrac{18}{5}\)