K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
8 tháng 5 2018
+) Nếu \(x< 2\Leftrightarrow|x-2|=2-x\)
\(|2-x|=2-x\)
\(pt\Leftrightarrow2-x+2-x=10\)
\(\Leftrightarrow-2x+4=10\)
\(\Leftrightarrow-2x=6\)
\(\Leftrightarrow x=-3\left(tm\right)\)
+) Nếu \(x\ge2\Leftrightarrow|x-2|=x-2\)
\(|2-x|=x-2\)
\(pt\Leftrightarrow x-2+x-2=10\)
\(\Leftrightarrow2x-4=10\)
\(\Leftrightarrow2x=14\)
\(\Leftrightarrow x=7\left(tm\right)\)
Vậy phương trình có tập nghiệm \(S=\left\{-3;7\right\}\)
DT
23 tháng 2 2022
áp dụng đl ta-lét vào tam giác có:
\(\dfrac{BC}{CA}=\dfrac{DE}{EA}=\dfrac{BC}{5}=\dfrac{3}{8}=>BC=\dfrac{3}{8}.5=\dfrac{15}{8}=1,875\)
X = BC + CA = 1,875 + 5 = 6,875
MT
1
31 tháng 7 2021
Ta có: \(\left(x-2\right)^{2020}\ge0\forall x\)
\(\left(y+5\right)^{2018}\ge0\forall y\)
Do đó: \(\left(x-2\right)^{2020}+\left(y+5\right)^{2018}\ge0\forall x,y\)
Dấu '=' xảy ra khi (x,y)=(2;-5)
NV
1
18 tháng 1 2022
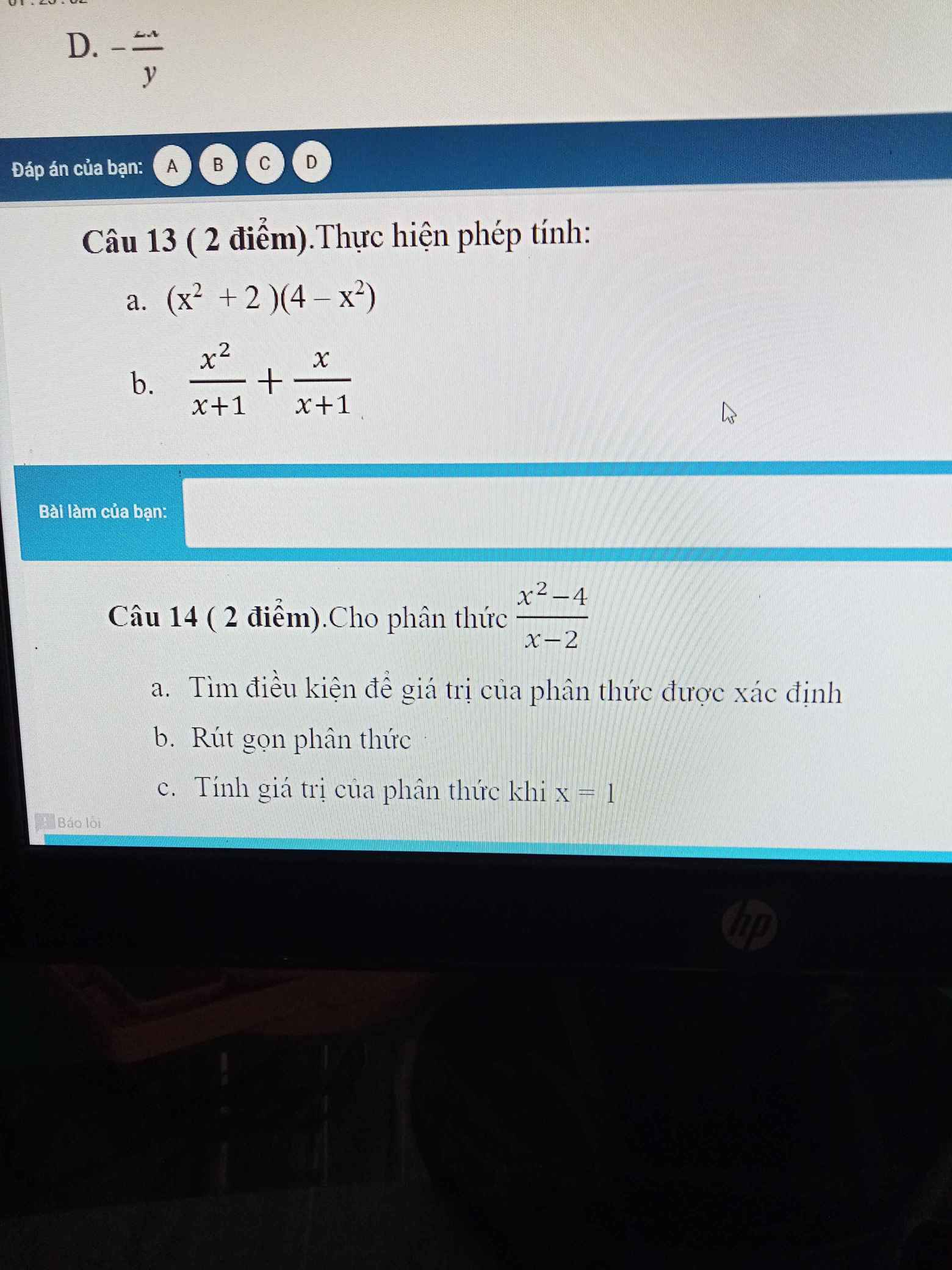
Câu 14;
a: ĐKXĐ: x<>2
b: \(\dfrac{x^2-4}{x-2}=x+2\)
c: Thay x=1 vào x+2, ta được:
x+2=1+2=3
17 tháng 10 2016
A= 2006 X 2008 - 20072
A = 2006 . 2008 - 2007 . 2007
A = 2006 . ( 2007 + 1 ) - 2007 . ( 2006 + 1 )
A = 2006 . 2007 + 2006 - 2007 . 2006 + 2007
A = -1
B= 2016 X 2018 - 20172
B= 2016 . 2018 - 2017 . 2017
B = 2016 . ( 2017 + 1 ) - 2017 . ( 2016 + 1 )
B = 2016 . 2017 + 2016 - 2017 . 2016 + 2017
B = -1
NH
1
KC
4