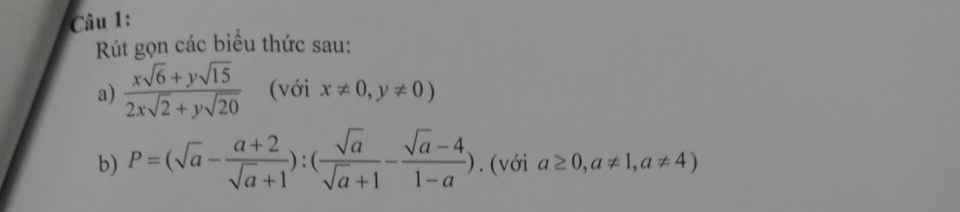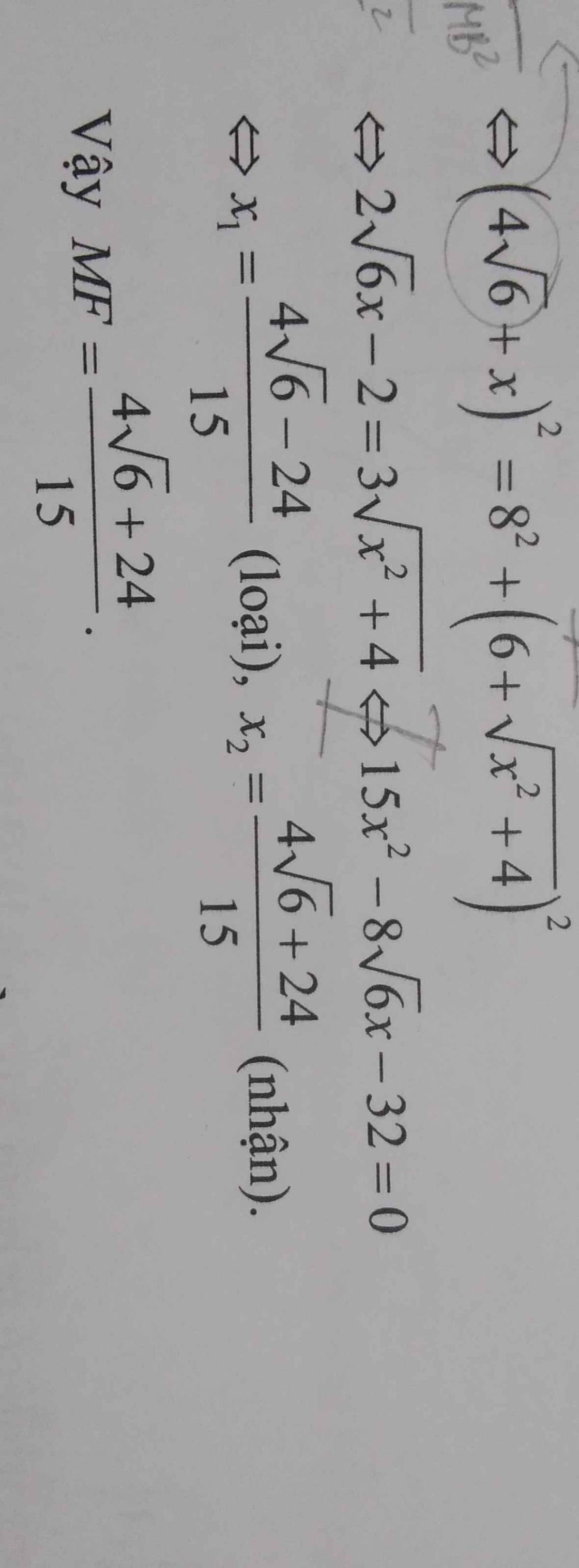Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp



a:
ΔOBC cân tại O
mà OI là trung tuyến
nên OI vuông góc BC
góc CMO+góc CIO=180 độ
=>CIOM nội tiếp

a: Khi x=2 thì (1) sẽ là:
4-2(m+2)+m+1=0
=>m+5-2m-4=0
=>1-m=0
=>m=1
x1+x2=m+1=3
=>x2=3-2=1
b: Δ=(m+2)^2-4(m+1)
=m^2+4m+4-4m-4=m^2>=0
=>Phương trình luôn có hai nghiệm
P=(x1+x2)^2-4x1x1+3x1x2
=(x1+x2)^2-x1x2
=(m+2)^2-m-1
=m^2+4m+4-m-1
=m^2+3m+3
=(m+3/2)^2+3/4>=3/4
Dấu = xảy ra khi m=-3/2

a: \(=\dfrac{\sqrt{3}\left(x\sqrt{2}+y\sqrt{5}\right)}{2\left(x\sqrt{2}+y\sqrt{5}\right)}=\dfrac{\sqrt{3}}{2}\)
b: \(=\dfrac{a+\sqrt{a}-a-2}{\sqrt{a}+1}:\dfrac{a-\sqrt{a}+\sqrt{a}-4}{a-1}\)
\(=\dfrac{\left(\sqrt{a}-2\right)}{\sqrt{a}+1}\cdot\dfrac{a-1}{a-4}=\dfrac{\sqrt{a}-1}{\sqrt{a}+2}\)

8: Ta có: \(\sqrt{6+2\sqrt{5}}-\dfrac{\sqrt{15}-\sqrt{3}}{\sqrt{3}}\)
\(=\sqrt{5}+1-\sqrt{5}+1\)
=2

`(4\sqrt{6}+x)^2=8^2+(6+\sqrt{x^2+4})^2`
`<=>96+8\sqrt{6}x+x^2=64+36+12\sqrt{x^2+4}+x^2+4`
`<=>2\sqrt{6}x-2=3\sqrt{x^2+4}` `ĐK: x >= \sqrt{6}/6`
`<=>24x^2-8\sqrt{6}x+4=9x^2+36`
`<=>15x^2-8\sqrt{6}x-32=0`
`<=>x^2-[8\sqrt{6}]/15x-32/15=0`
`<=>(x-[4\sqrt{6}]/15)^2-64/25=0`
`<=>|x-[4\sqrt{6}]/15|=8/5`
`<=>[(x=[24+4\sqrt{6}]/15 (t//m)),(x=[-24+4\sqrt{6}]/15(ko t//m)):}`
 người giúp em bài này được không ạ ....
người giúp em bài này được không ạ ....