Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 5:
a) \(23⋮\left(x-2\right)\Leftrightarrow x-2\inƯ\left(23\right)=\left\{-23,-1,1,23\right\}\)
\(\Leftrightarrow x\in\left\{-21,1,3,25\right\}\).
b) \(2x+1\inƯ\left(-12\right)\)mà \(2x+1\)là số lẻ nên \(2x+1\in\left\{-3,-1,1,3\right\}\)
\(\Leftrightarrow x\in\left\{-2,-1,0,1\right\}\).
c) \(x-1=x+2-3⋮\left(x+2\right)\Leftrightarrow3⋮\left(x+2\right)\)
mà \(x\)là số nguyên nên \(x+2\inƯ\left(3\right)=\left\{-3,-1,1,3\right\}\Leftrightarrow x\in\left\{-5,-3,-1,1\right\}\).
Bài 4:
a) \(-18⋮3,15⋮3\Rightarrow-18a+15b⋮3\).
b) Theo a) ta có \(-18a+15b⋮3\)mà \(-2015⋮̸3\)nên không tồn tại hai số nguyên \(a,b\)thỏa mãn ycbt.

Bài 4:
a. Ta có: $-18a+15b=3(-6a+5b)\vdots 3$
b. Vì $-18a+15b$ chia hết cho $3$ với $a,b$ nguyên, mà $-2015\not\vdots 3$ nên không tồn tại hai số $a,b$ nguyên thỏa mãn $-18a+15b=-2015$
Bài 5:
a.
$23\vdots x-2$
$\Rightarrow x-2\in$ Ư$(23)$
$\Rightarrow x-2\in\left\{\pm 1;\pm 23\right\}$
$\Rightarrow x\in\left\{3; 1; 25; -21\right\}$
b.
$2x+1\in$ Ư$(-12)$, mà $2x+1$ lẻ nên:
$2x+1\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow x\in\left\{0; -1; 1; -2\right\}$
c.
$x-1\vdots x+2$
$(x+2)-3\vdots x+2$
$3\vdots x+2$
$\Rightarrow x+2\in$ Ư$(3)$
$\Rightarrow x+2\in\left\{\pm 1;\pm 3\right\}$
$\Rightarrow x\in\left\{-1; -3; -5; 1\right\}$


TL:
\(2x^3+16=32\)
\(2x^3=32-16\)
\(2x^3=16\)
\(x^3=16:2\)
\(x^3=8\)
\(x^3=2^3\)
\(\Rightarrow x=2\)
HT!~!


b/3^8x+4=81^3=(3^4)^3=3^12
--->8x+4=12->8x=8-->x=1
dấu "^" là dấu lũy thừa đó bạn

59007=3x13x17x89
b là tháng \(\Rightarrow b\le12\Rightarrow b=3\)
a là ngày => a={13;17} => c=89
tuổi long là
2002-1989=13 tuổi
Vậy long sinh ngày 17/03/1989
Nguyễn Ngọc Anh Minh, giải còn thiếu 1 trường hợp nhưng mình k cho bạn nhé:))



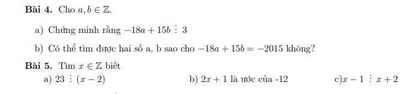
 Làm giúp tui nhé cảm ơn mọi người rất nhìu !
Làm giúp tui nhé cảm ơn mọi người rất nhìu !



 Làm giúp tui nha. Cảm ơn mọi người rất nhiều !
Làm giúp tui nha. Cảm ơn mọi người rất nhiều !
Bài 4:
a) \(x+xy-3y=4\)
\(\Leftrightarrow x-3+y\left(x-3\right)=1\)
\(\Leftrightarrow\left(x+y\right)\left(x-3\right)=1\)
mà \(x.y\)là số nguyên nên ta có bảng giá trị:
b) \(BCNN\left(6,7\right)=42\)nên \(BC\left(6,7\right)=B\left(42\right)\).
\(200< 6k< 2000\Rightarrow33< k< 334\)
suy ra có \(334-33-1=300\)giá trị của \(x\)là bội của \(6\)mà \(200< x< 2000\).
\(200< 7l< 2000\Rightarrow28< l< 286\)
suy ra có \(286-28-1=257\)giá trị của \(x\)là bội của \(7\)mà \(200< x< 2000\).
\(200< 42m< 2000\Leftrightarrow4< m< 48\)
suy ra có \(48-4-1=43\)giá trị của \(x\)là bội của \(42\)mà \(200< x< 2000\)
Số giá trị của \(x\)thỏa mãn ycbt là: \(300+257-43=514\)(số)