K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PB
3
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 7 2021
6.4
\(y=\dfrac{3}{2}\left(1+cos2x\right)-\sqrt{3}sin2x+\dfrac{1}{2}-\dfrac{1}{2}cos2x\)
\(=cos2x-\sqrt{3}sin2x+2\)
\(=2\left(\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x\right)+2\)
\(=2cos\left(2x-\dfrac{\pi}{3}\right)+2\)
Do \(-1\le cos\left(2x-\dfrac{\pi}{3}\right)\le1\)
\(\Rightarrow0\le y\le4\)
\(y_{min}=0\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=-1\)
\(y_{max}=4\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=1\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 7 2021
6.5
Ủa nhìn bài 7 thì đây là chương trình lớp 11 (pt lượng giác) chứ đâu phải lớp 10?
Vậy giải theo kiểu lớp 11 nghe:
\(y=\dfrac{2+cosx+3sinx}{2+cosx}\)
\(\Leftrightarrow2y+y.cosx=2+cosx+3sinx\)
\(\Leftrightarrow3sinx+\left(1-y\right).cosx=2y-2\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(9+\left(1-y\right)^2\ge\left(2y-2\right)^2\)
\(\Leftrightarrow\left(y-1\right)^2\le3\)
\(\Rightarrow1-\sqrt{3}\le y\le1+\sqrt{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 4 2021
a. Gọi \(x_1>x_2\) là 2 nghiệm của \(x^2+6x+m+7=0\) thì BPT đã cho có tập nghiệm là đoạn có chiều dài bằng 1 khi và chỉ khi \(x_1-x_2=1\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=1\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=1\)
\(\Leftrightarrow36-4\left(m+7\right)=1\)
\(\Leftrightarrow m=\dfrac{7}{4}\)
b. \(x^2+6x+m+7\le0\) ;\(\forall x\in\left[-4;-1\right]\)
\(\Leftrightarrow x^2+6x+7\le-m\) ; \(\forall x\in\left[-4;-1\right]\)
\(\Leftrightarrow-m\ge\max\limits_{\left[-4;-1\right]}\left(x^2+6x+7\right)\)
Xét hàm \(f\left(x\right)=x^2+6x+7\) trên \(\left[-4;-1\right]\)
\(-\dfrac{b}{2a}=-3\in\left[-4;-1\right]\) ; \(f\left(-4\right)=-1\) ; \(f\left(-3\right)=-2\) ; \(f\left(-1\right)=2\)
\(\Rightarrow\max\limits_{\left[-4;-1\right]}\left(x^2+6x+7\right)=2\Rightarrow-m\ge2\)
\(\Rightarrow m\le-2\)
7 tháng 1 2022
c: \(\Leftrightarrow x^2-5x-x^2-7< =0\)
=>-5x<=7
hay x>=-7/5
d: \(\Leftrightarrow x^2-x-2+3-x^2>=0\)
=>-x+1>=0
=>-x>=-1
hay x<=1
AH
Akai Haruma
Giáo viên
25 tháng 10 2021
Lời giải:
a. TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(x)=|x|=|-x|=f(-x)$
$\Rightarrow $ hàm chẵn
b. TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=9; -f(1)=-9; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$ nên hàm không chẵn không lẻ.
c.
TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(-x)=(-x)^3+(-x)=-(x^3+x)=-f(x)$ nên hàm lẻ
d.
TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=3; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$
Do đó hàm không chẵn không lẻ.
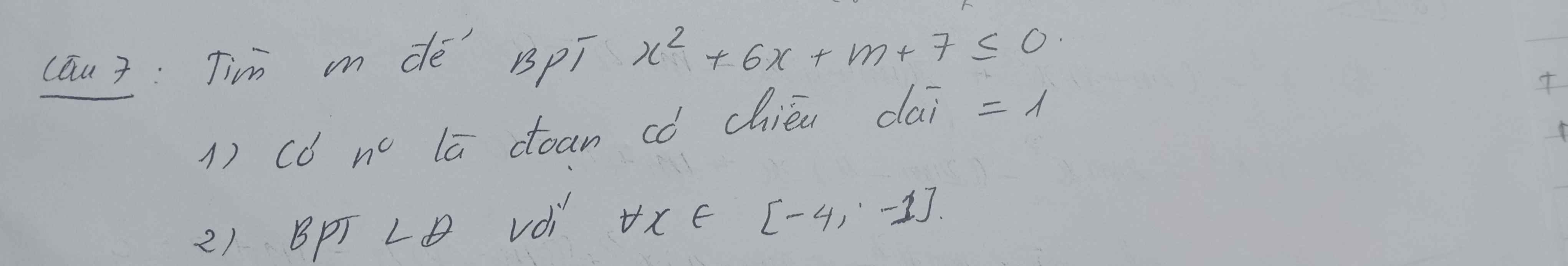
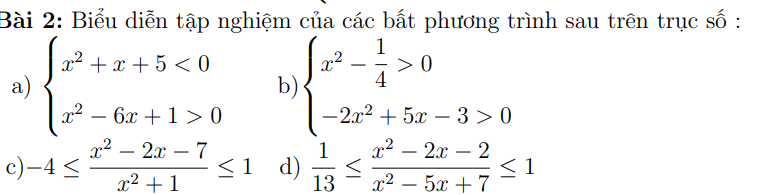
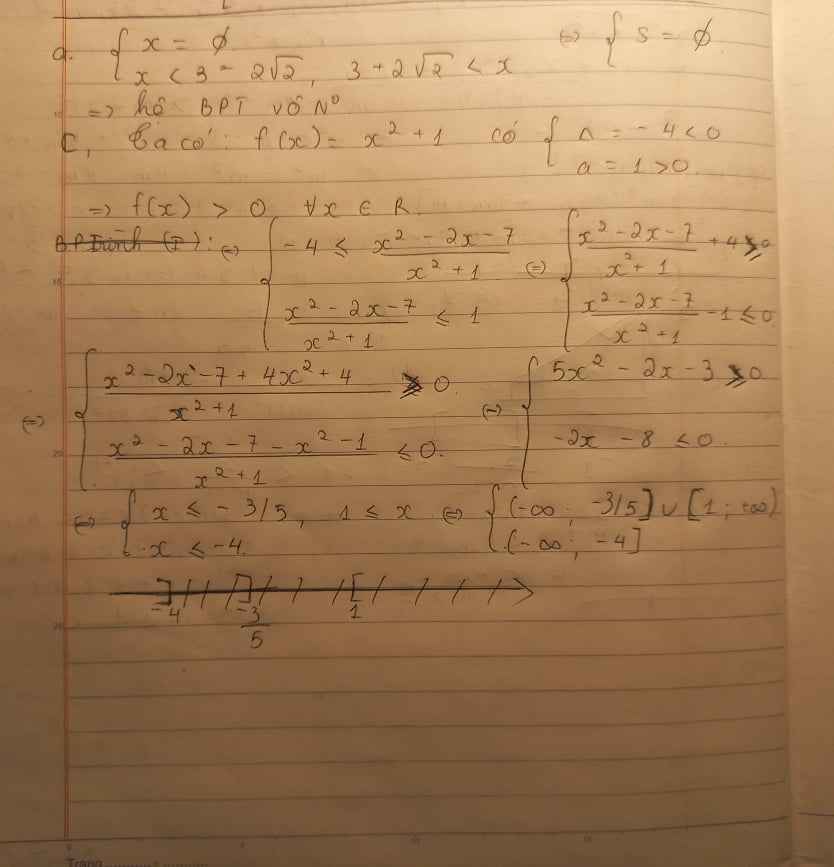
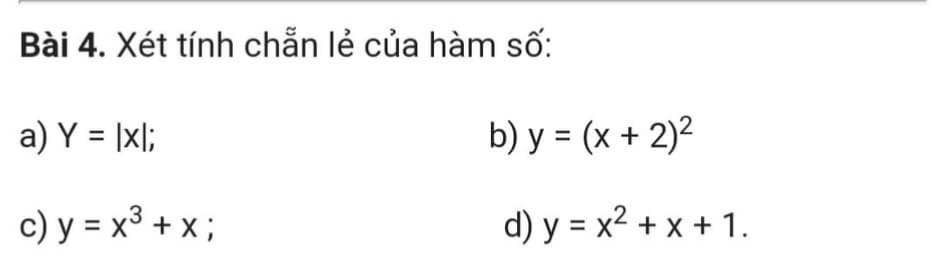
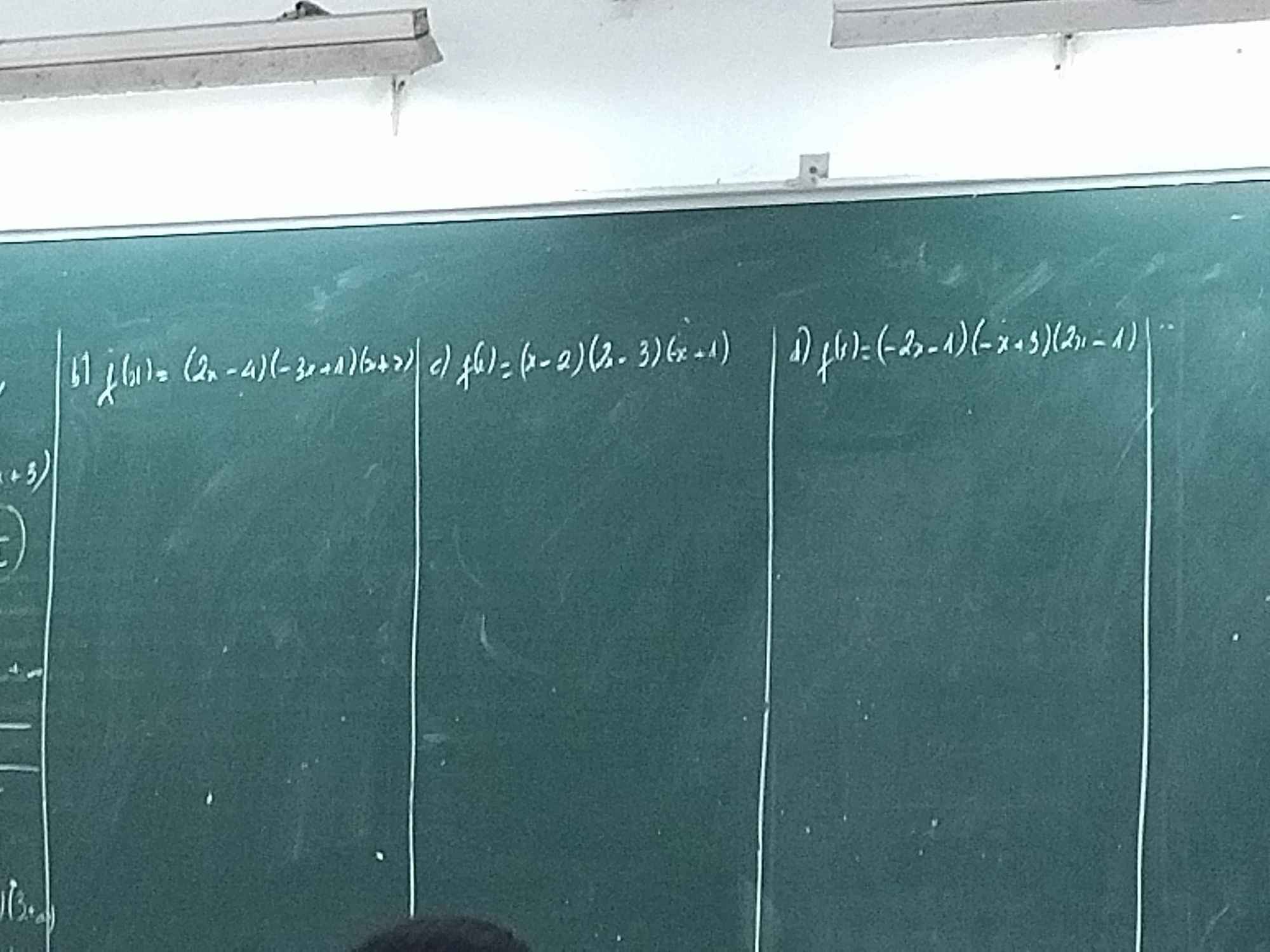
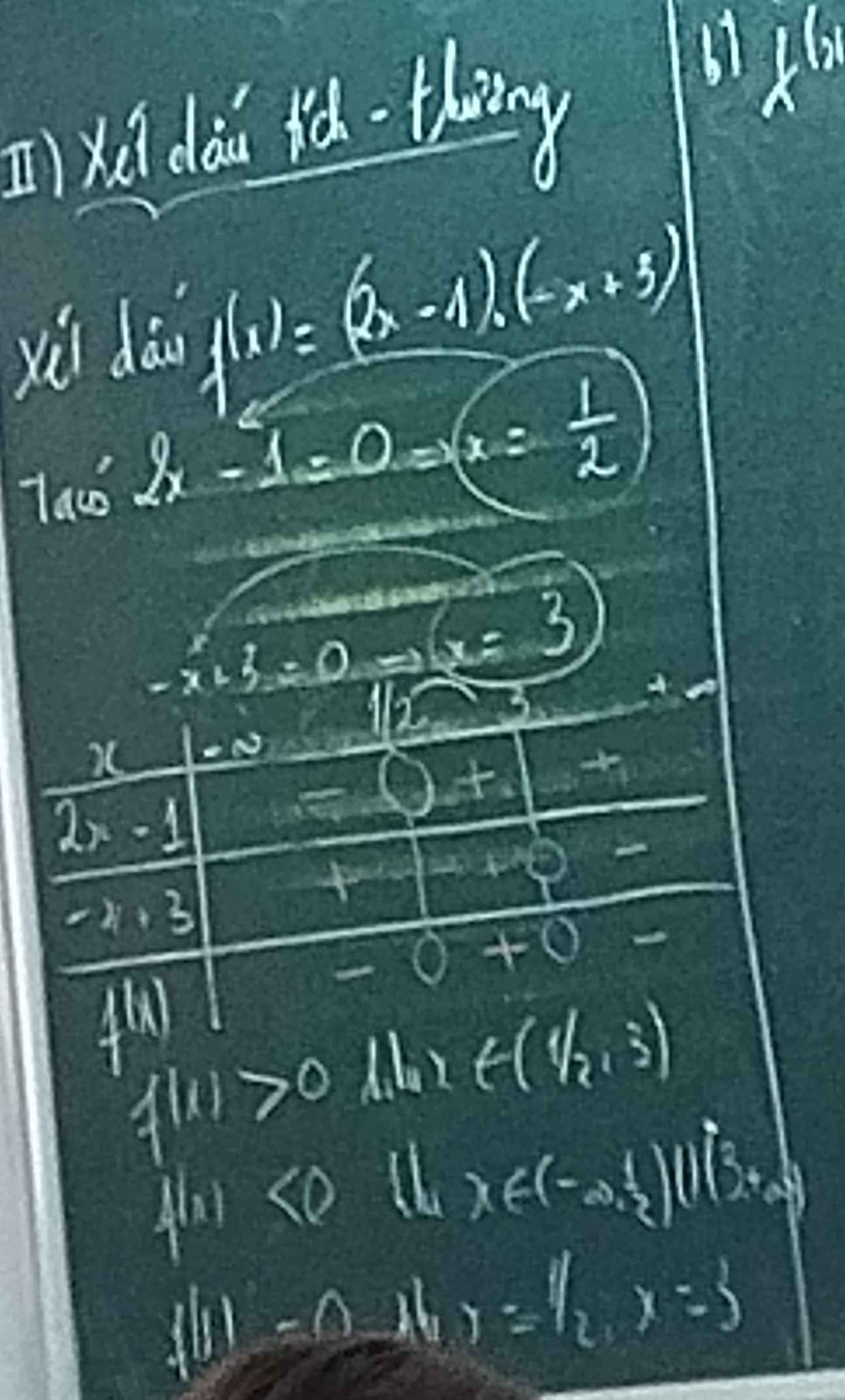
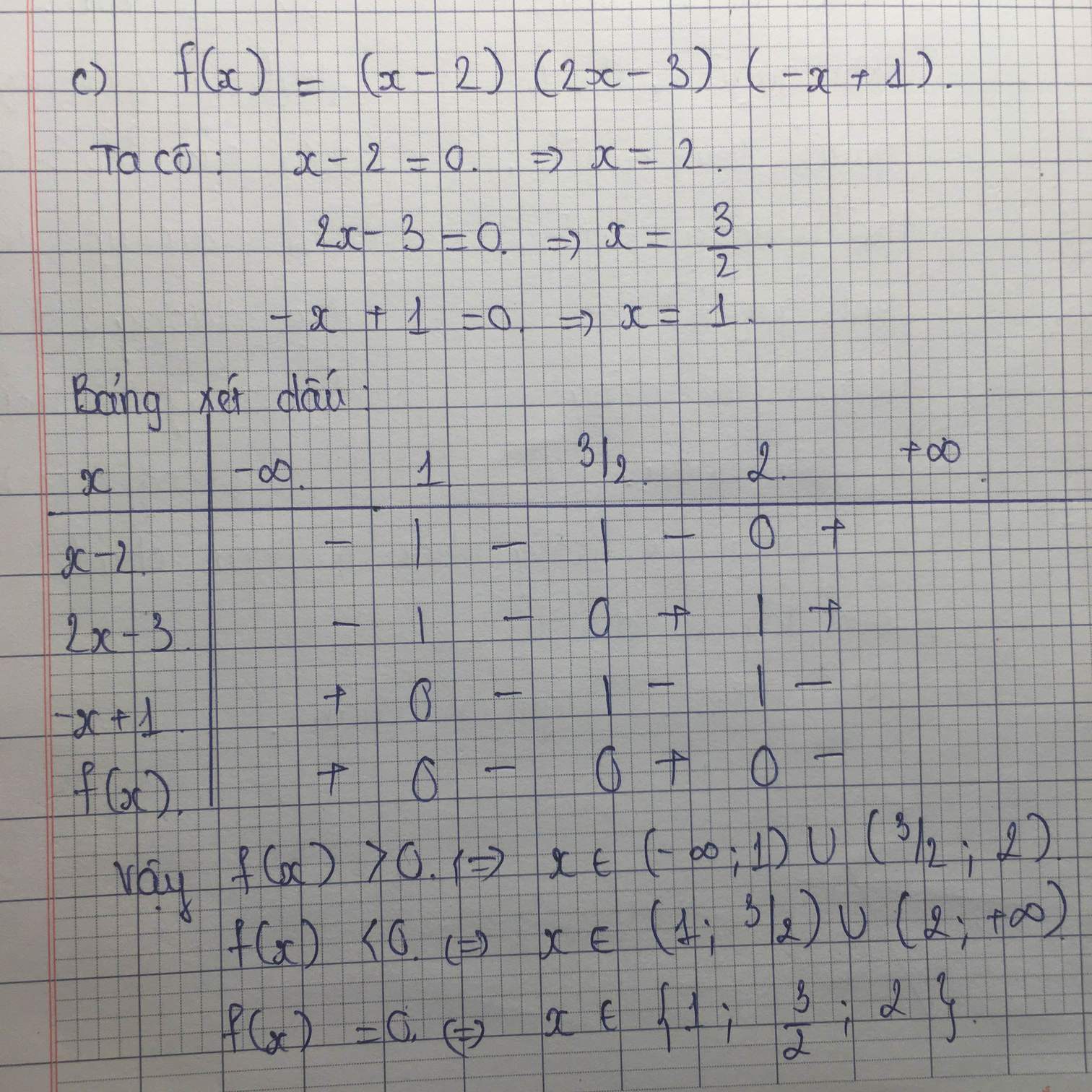
\(\left(m-2\right)x^4-2\left(m+1\right)x^2+2m-1=0\left(1\right)\)
\(m=2\left(ktm\right)\)
\(m\ne2:đặt:x^2=t\ge0\Rightarrow\left(1\right)\Leftrightarrow\left(m-2\right)t^2-2\left(m+1\right)t+2m-1=0\)
\(3nghiem\Leftrightarrow\left\{{}\begin{matrix}2m-1=0\\t1+t2=\dfrac{2m+2}{m-2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{2}\\\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m\in\phi\)
\(4nghiem\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\t1+t2>0\Leftrightarrow\\t1.t2>0\end{matrix}\right.\left\{{}\begin{matrix}\left(m+1\right)^2-\left(m-2\right)\left(2m-1\right)>0\\\dfrac{2m+2}{m-2}>0\\\dfrac{2m-1}{m-2}>0\end{matrix}\right.\)
giải hệ bất pt trên=>m
\(c3:b;\left\{{}\begin{matrix}-8\le x\le-2\\m\left(x-3\right)\ge1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}-8\le x\le-2\\m\le\dfrac{1}{x-3}\end{matrix}\right.\)
\(có\) \(nghiệm\Leftrightarrow m\le max:\dfrac{1}{x-3}trên\left[-8;-2\right]\)
\(\Leftrightarrow m\le\dfrac{-1}{5}\)