
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HV
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên
CD
0

NT
0

ML
2

NH
2

28 tháng 8 2021
Mình trình bày cho dễ hiểu nha
\(sina-\sqrt{3}cosa\)
\(=2\cdot\left(\frac{1}{2}sina-\frac{\sqrt{3}}{2}cosa\right)\)
\(=2\cdot\left(sinacos\frac{pi}{6}-cosasin\frac{pi}{6}\right)\)
\(=2\cdot sin\left(a-\frac{pi}{6}\right)\)
Ta có\(-1\le sin\left(a-\frac{pi}{6}\right)\le1\)
\(-2\le sin\left(a-\frac{pi}{6}\right)\le2\)
Vậy Min=-2
Max=2
NV
0

QN
0

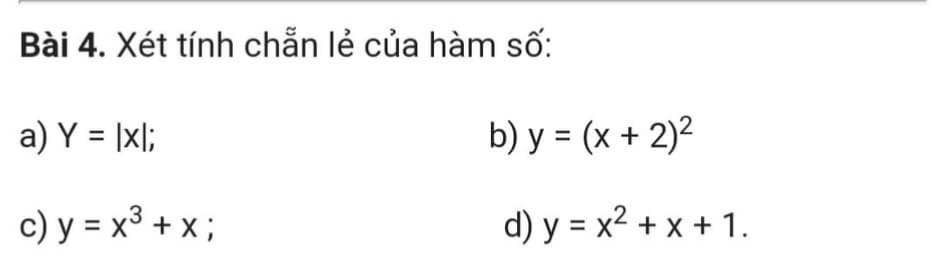



 Em không hiểu gộp làm sao lại ra được kết quả như vậy ấy ạ.
Em không hiểu gộp làm sao lại ra được kết quả như vậy ấy ạ. 

 mượn cái ngầu lòi của hai người này ới đấy đi học oln hahaha
mượn cái ngầu lòi của hai người này ới đấy đi học oln hahaha



Lời giải:
a. TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(x)=|x|=|-x|=f(-x)$
$\Rightarrow $ hàm chẵn
b. TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=9; -f(1)=-9; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$ nên hàm không chẵn không lẻ.
c.
TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(-x)=(-x)^3+(-x)=-(x^3+x)=-f(x)$ nên hàm lẻ
d.
TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=3; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$
Do đó hàm không chẵn không lẻ.