K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 6 2021
\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{3}=\dfrac{\pi}{6}+k2\pi\\2x+\dfrac{\pi}{3}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+k\pi\\x=\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất là \(x=\dfrac{\pi}{4}\approx0.79\)
Đáp án C
PN
0
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2022
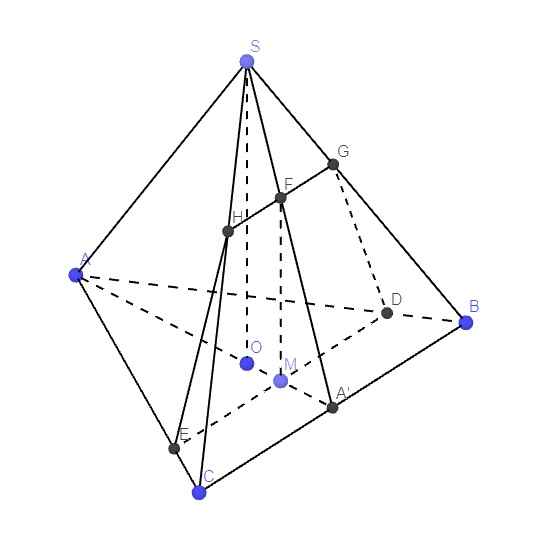
\(\left\{{}\begin{matrix}SO\perp BC\\SO\perp CA\end{matrix}\right.\) \(\Rightarrow SO\perp\left(ABC\right)\)
\(AA'=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều) \(\Rightarrow AO=\dfrac{2}{3}AA'=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow M\) nằm trên đoạn thẳng OA'
Qua M kẻ đường thẳng song song BC cắt AB và AC lần lượt tại D và E
Trong mp (SAA'), qua M kẻ đường thẳng song song SO cắt SA' tại F
Trong mp (SBC), qua F kẻ đường thẳng song song BC cắt SB và SC lần lượt tại G và H
\(\Rightarrow\) Hình thang DEHG là thiết diện của (P) và chóp
\(FM||SO\Rightarrow FM\perp\left(ABC\right)\Rightarrow FM\perp ED\)
Áp dụng định lý Talet cho tam giác ABC:
\(\dfrac{DE}{BC}=\dfrac{AM}{AA'}\Rightarrow DE=\dfrac{BC.AM}{AA'}=\dfrac{a.x}{\dfrac{a\sqrt{3}}{2}}=\dfrac{2x\sqrt{3}}{3}\)
Talet tam giác SOA':
\(\dfrac{FM}{SO}=\dfrac{MA'}{OA'}\Rightarrow FM=\dfrac{SO.MA'}{OA'}=\dfrac{2a.\left(\dfrac{a\sqrt{3}}{2}-x\right)}{\dfrac{a\sqrt{3}}{6}}=6a-4\sqrt{3}x\)
Talet tam giác SBC:
\(\dfrac{GH}{BC}=\dfrac{SF}{SA'}=1-\dfrac{FA'}{SA'}=1-\dfrac{FM}{SO}=1-\dfrac{6a-4\sqrt{3}x}{2a}=\dfrac{2\sqrt{3}x-2a}{a}\)
\(\Rightarrow GH=2\sqrt{3}x-2a\)
\(S_{DEHG}=\dfrac{1}{2}\left(DE+GH\right).FM=\dfrac{1}{2}\left(\dfrac{2x\sqrt{3}}{3}+2\sqrt{3}x-2a\right)\left(6a-4\sqrt{3}x\right)\)
\(=\dfrac{1}{3}\left(4\sqrt{3}x-3a\right)\left(6a-4\sqrt{3}x\right)\le\dfrac{1}{12}\left(4\sqrt{3}x-3a+6a-4\sqrt{3}x\right)^2=\dfrac{9a^2}{12}\)
Dấu "=" xảy ra khi \(4\sqrt{3}x-3a=6a-4\sqrt{3}x\Leftrightarrow x=\dfrac{9a}{8\sqrt{3}}=\dfrac{3a\sqrt{3}}{8}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2022
Do M là trung điểm SA, N là trung điểm AC
\(\Rightarrow\) MN là đường trung bình tam giác SAC
\(\Rightarrow MN||SC\)
Mà \(SC\in\left(SCD\right)\Rightarrow MN||\left(SCD\right)\)
PA
1
4 tháng 3 2023
\(=\lim\limits_{x->2}\dfrac{3x-2-4}{\sqrt{3x-2}+2}\cdot\dfrac{1}{-2\left(x-2\right)}\)
\(=\lim\limits_{x->2}\dfrac{-3}{2\left(\sqrt{3x-2}+2\right)}=\dfrac{-3}{2\sqrt{3\cdot2-2}+4}=\dfrac{-3}{8}\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 7 2021
a.
\(90^0< a< 180^0\Rightarrow cosa< 0\)
\(\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{2\sqrt{2}}{3}\)
\(tana=\dfrac{sina}{cosa}=-\dfrac{\sqrt{2}}{4}\)
b.
\(0< a< 90^0\Rightarrow cosa>0\)
\(\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{4}{5}\)
\(tana=\dfrac{sina}{cosa}=\dfrac{3}{4}\)
\(cota=\dfrac{1}{tana}=\dfrac{4}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 7 2021
c.
\(A=\dfrac{\dfrac{sina}{cosa}+\dfrac{3cosa}{sina}}{\dfrac{sina}{cosa}+\dfrac{cosa}{sina}}=\dfrac{sin^2a+3cos^2a}{sin^2a+cos^2a}=1+2cos^2a=\dfrac{17}{8}\)
d.
\(A=\dfrac{\dfrac{cosa}{sina}+\dfrac{3sina}{cosa}}{\dfrac{2cosa}{sina}+\dfrac{sina}{cosa}}=\dfrac{cos^2a+3sin^2a}{2cos^2a+sin^2a}=\dfrac{cos^2a+3\left(1-cos^2a\right)}{2cos^2a+\left(1-cos^2a\right)}\)
\(=\dfrac{3-2cos^2a}{1+cos^2a}=\dfrac{19}{13}\)
HP
13 tháng 7 2021
11.
\(sin^2x-4sinx.cosx+3cos^2x=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-3cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx-cosx=0\\sinx-3cosx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=3cosx\end{matrix}\right.\)
Với \(cosx=0\Rightarrow\) pt vô nghiệm
Với \(cosx\ne0\)
\(pt\Leftrightarrow\left[{}\begin{matrix}tanx=0\\tanx=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=arctan3+k\pi\end{matrix}\right.\)
20 tháng 12 2021
Trong mp (ABCD), nối AN kéo dài cắt BC kéo dài tại E
⇒E∈(SBC)⇒E∈(SBC)
Do AD song song BE, áp dụng Talet:
ANNE=NDNC=1⇒AN=NE⇒ANNE=NDNC=1⇒AN=NE⇒ N là trung điểm AE
⇒MN⇒MN là đường trung bình tam giác SAE
⇒MN//SE⇒MN//(SBC)
3.
a. Mỗi vị trí có 8 cách chọn, do đó có thể lập \(3^8\) chữ số
b. Số số thỏa mãn: \(8.7.6=...\)
c. Chữ số hàng đơn vị phải là số chẵn \(\Rightarrow\) có 4 cách chọn
Hai chữ số còn lại có \(7.6\) cách
Tổng: \(4.7.6=...\)
d. Chia X làm 3 tập: \(A=\left\{3;6\right\}\) gồm các chữ số chia hết cho 3
\(B=\left\{1;4;7\right\}\) gồm các số chia 3 dư 1
\(C=\left\{2;5;8\right\}\) gồm các số chia 3 dư 2
Số được lập thỏa mãn khi các TH sau xảy ra: (3 số được chọn nằm cùng 1 tập), (3 số được chọn nằm ở 3 tập khác nhau)
\(\Rightarrow3!+3!+3!.C_2^1.C_3^1.C_3^1=...\)
4.
Gọi chữ số cần lập là \(\overline{abc}\)
a.
a có 6 cách chọn, b và c mỗi vị trí có 7 cách chọn
\(\Rightarrow6.7.7=...\) số
b.
a có 6 cách chọn (khác 0), b có 6 cách chọn (khác a), c có 5 cách chọn (khác a và b)
\(\Rightarrow6.6.5=...\) số
c.
- Nếu \(c=0\Rightarrow\) a có 6 cách chọn, b có 5 cách chọn \(\Rightarrow6.5\) số
- Nếu \(c\ne0\Rightarrow c\) có 3 cách chọn (2;4;6), a có 5 cách chọn (khác c và 0), b có 5 cách chọn (khác a và c) \(\Rightarrow3.5.5\) số
Tổng cộng: \(6.5+3.5.5=...\) số