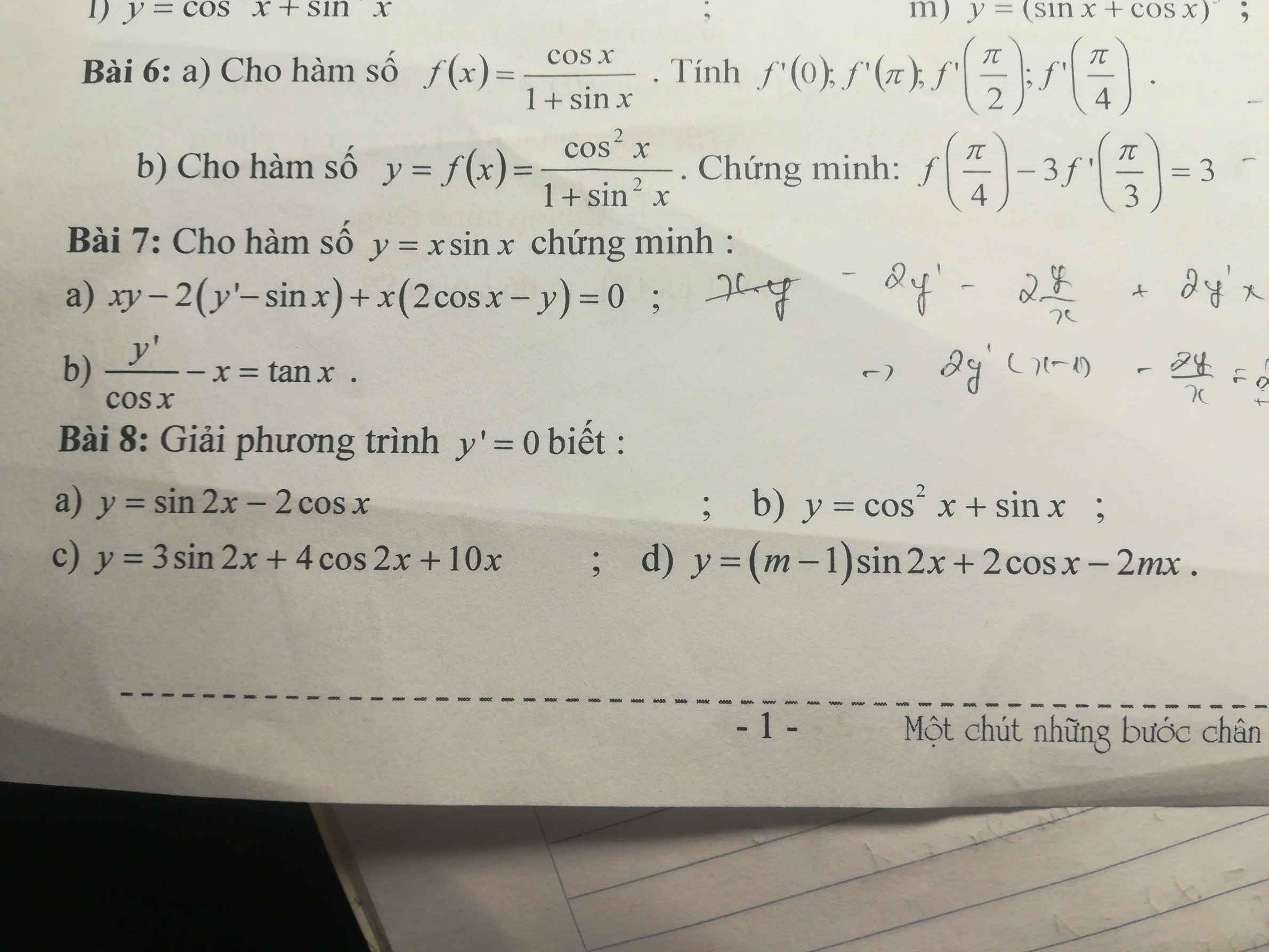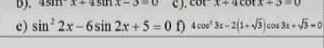Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y'=\left(m-1\right)\cos2x\cdot2-2\cdot\sin x-2m=0\)
\(\Leftrightarrow\left(m-1\right)\left(1-2\sin^2x\right)-\sin x-m=0\)
\(\Leftrightarrow2\left(1-m\right)\sin^2x-\sin x-1=0\)
bạn tự làm nốt nha



11.
\(sin^2x-4sinx.cosx+3cos^2x=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-3cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx-cosx=0\\sinx-3cosx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=3cosx\end{matrix}\right.\)
Với \(cosx=0\Rightarrow\) pt vô nghiệm
Với \(cosx\ne0\)
\(pt\Leftrightarrow\left[{}\begin{matrix}tanx=0\\tanx=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=arctan3+k\pi\end{matrix}\right.\)


e) \(sin^22x-6sin2x+5=0\Rightarrow\) \(\left[{}\begin{matrix}sin2x=5\left(loại\right)\\sin2x=1\end{matrix}\right.\)
\(\Rightarrow sin2x=sin\left(\dfrac{\pi}{2}\right)\)
\(\Rightarrow2x=\dfrac{\pi}{2}+k2\pi\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
f.
\(4cos^23x-2\left(\sqrt{3}+1\right)cos3x+\sqrt{3}=0\)
\(\Leftrightarrow4cos^23x-2cos3x-2\sqrt{3}cos3x+\sqrt{3}=0\)
\(\Leftrightarrow2cos3x\left(2cos3x-1\right)-\sqrt{3}\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left(2cos3x-\sqrt{3}\right)\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=\dfrac{1}{2}\\cos3x=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)

\(f'\left(x\right)=x^2+2x\)
a.
\(f'\left(-3\right)=3\) ; \(f\left(-3\right)=-2\)
Phương trình tiếp tuyến:
\(y=3\left(x+3\right)-2\Leftrightarrow y=3x+7\)
b.
Gọi \(x_0\) là hoành độ tiếp điểm, do hệ số góc tiếp tuyến bằng 3
\(\Rightarrow f'\left(x_0\right)=3\Rightarrow x_0^2+2x_0=3\Rightarrow x_0^2+2x_0-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=1\Rightarrow y_0=-\dfrac{2}{3}\\x_0=-3\Rightarrow y_0=-2\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=3\left(x-1\right)-\dfrac{2}{3}=3x-\dfrac{11}{3}\\y=3\left(x+3\right)-2=3x+7\end{matrix}\right.\)
c. Tiếp tuyến song song (d) nên có hệ số góc bằng 8
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow x_0^2+2x_0=8\)
\(\Rightarrow\left[{}\begin{matrix}x_0=2\Rightarrow y_0=\dfrac{14}{3}\\x_0=-4\Rightarrow y_0=-\dfrac{22}{3}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=8\left(x-2\right)+\dfrac{14}{3}=...\\y=8\left(x+4\right)-\dfrac{22}{3}=...\end{matrix}\right.\)

\(y'=\dfrac{-5}{\left(x-3\right)^2}\)
\(\Rightarrow y'\left(4\right)=\dfrac{-5}{\left(4-3\right)^2}=-5\) ; \(y\left(4\right)=\dfrac{2.4-1}{4-3}=7\)
Phương trình tiếp tuyến tại điểm có hoành độ \(x=4\) là:
\(y=-5\left(x-4\right)+7=-5x+27\)

\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{3}=\dfrac{\pi}{6}+k2\pi\\2x+\dfrac{\pi}{3}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+k\pi\\x=\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất là \(x=\dfrac{\pi}{4}\approx0.79\)
Đáp án C