K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 5 2022
a,
Xét Δ ABH và Δ CBA, có :
\(\widehat{ABH}=\widehat{CAB}\) (góc chung)
\(\widehat{AHB}=\widehat{CAB}=90^o\)
=> Δ ABH ~ Δ CBA (g.g)
=> \(\dfrac{AB}{CB}=\dfrac{BH}{BA}\)
=> \(AB^2=BH.BC\)
Xét Δ ABC vuông tại A, có :
\(BC^2=AB^2+AC^2\) (Py - ta - go)
=> \(BC^2=15^2+20^2\)
=> BC = 25 (cm)
Ta có : \(AB^2=BH.BC\) (cmt)
=> \(15^2=BH.25\)
=> BH = 9 (cm)
Ta có : BC = BH + CH
=> 25 = 9 + CH
=> CH = 16 (cm)
26 tháng 5 2022
b,
Xét Δ AMN và Δ ACB, có :
\(\widehat{MAN}=\widehat{CAB}=90^o\)
\(\widehat{MAN}=\widehat{CAB}\) (góc chung)
=> Δ AMN ~ Δ ACB (g.g)
=> \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> AM.AB = AN.AC
Ta có : \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> \(\dfrac{AB}{AC}=\dfrac{AN}{AM}\)
=> \(\dfrac{AN}{AM}=\dfrac{15}{20}=\dfrac{3}{4}\)
Vậy : ta có kết luận : Δ AMN = \(\dfrac{3}{4}\) Δ ACB
8 tháng 9 2021
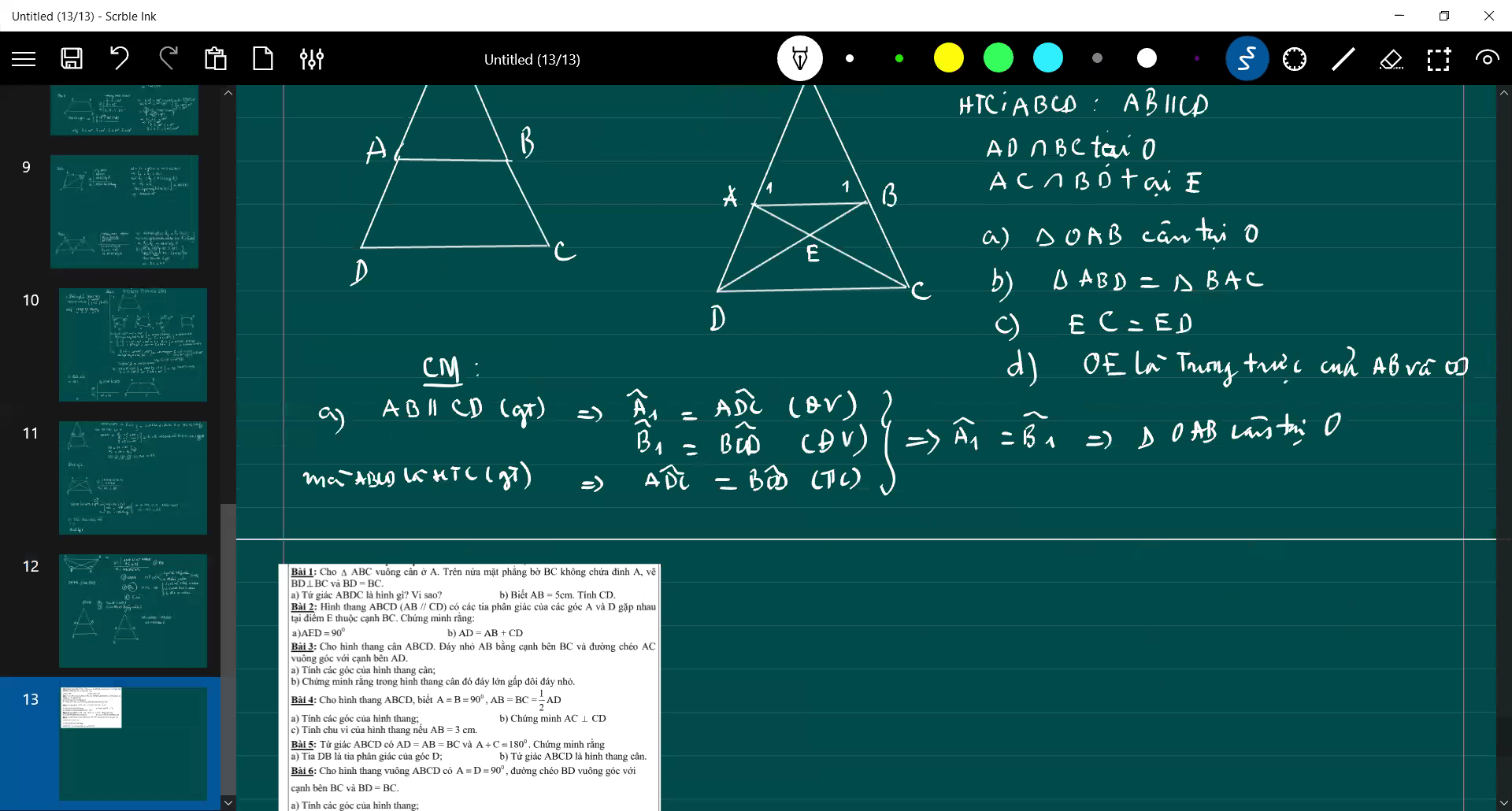
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ta có: EA+EC=AC
EB+ED=BD
mà AC=BD
và EA=EB
nên EC=ED
3 tháng 10 2021
a: Xét tứ giác AMHN có
\(\widehat{MAN}=\widehat{ANH}=\widehat{AMH}=90^0\)
Do đó: AMHN là hình chữ nhật
3 tháng 10 2021
a) Xét tứ giác AMHN có:
\(\widehat{AMH}=\widehat{MAN}=\widehat{ANH}=90^0\)
=> AMHN là hình chữ nhật
b) Ta có: MH=AN(AMHN là hình chữ nhật)
AN=DN(D đối xứng với A qua N)
=> MH=DN
MH//DN(AMHN là hình chữ nhật nên MH//AN,D∈AN)
=> MHDN là hình bình hành
11 tháng 5 2022
Ta có: \(\dfrac{x-2}{x-1}< =0\)
nên x-1>0 và x-2<=0
=>1<x<=2
LN
0
30 tháng 3 2022
a: \(\Leftrightarrow4\left(2x+1\right)-3\left(6x-1\right)=2x+1\)
=>8x+4-18x+3=2x+1
=>-10x+7=2x+1
=>-12x=-6
hay x=1/2
b: \(\Leftrightarrow4x^2-12x+7x-21-x^2=3x^2+6x\)
=>5x-21=6x
=>-x=21
hay x=-21
4 tháng 1 2022
a: Xét tứ giác ABDM có
DM//AB
AM//DB
Do đó: ABDM là hình bình hành
b: Xét ΔCAB và ΔCDB có
CA=CD
BA=BD
CB chung
Do đó: ΔCAB=ΔCDB
Suy ra: \(\widehat{CAB}=\widehat{CDB}=90^0\)
hay BD⊥DC
18 tháng 6 2021
câu 6:
a,áp dụng pytago\(=>BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10cm\)
do \(\Delta ABC\) vuông tại A có AM là trung tuyến
\(=>AM=\dfrac{1}{2}BC=\dfrac{1}{2}.10=5cm\)
b, xét \(\Delta ABC\) và \(\Delta HBA\) có: \(\angle\left(B\right)\) chung
\(\angle\left(A\right)=\angle\left(AHB\right)=90^o\)\(=>\Delta ABC\sim\Delta HBA\left(g.g\right)\)
\(=>\dfrac{AB}{HB}=\dfrac{BC}{AB}=>AB^2=HB.BC\)
c, điểm K trong đề bài không có bạn ơi.
18 tháng 6 2021
Câu 8:
a, \(xét\) \(\Delta ABH\) và \(\Delta CBA\) có: \(\angle\left(B\right)chung\)
\(\angle\left(A\right)=\angle\left(AHB\right)=90^0\)\(=>\Delta ABH\sim\Delta CBA\left(g.g\right)\)
\(=>\dfrac{AB}{BC}=\dfrac{BH}{AB}< =>AB^2=BH.BC\)
b,\(\) có \(\angle\left(B\right)+\angle\left(C\right)=90^o\)
mà \(\angle\left(C\right)+\angle\left(HAC\right)=90^o=>\angle\left(HAC\right)=\angle\left(B\right)\)
mà \(\angle\left(AHB\right)=\angle\left(AHC\right)=90^o\)
\(=>\Delta AHB\sim\Delta CHA\left(g.g\right)\)
\(=>\dfrac{AH}{CH}=\dfrac{HB}{AH}=>AH^2=HB.CH\)
c, ta có \(BD\) là phân giác\(=>\angle\left(ABD\right)=\angle\left(HBI\right)\)
mà \(\angle\left(A\right)=\angle\left(IHB\right)=90^0=>\Delta ABD\sim\Delta HBI\left(g.g\right)\)
\(=>\dfrac{AB}{HB}=\dfrac{AD}{HI}=>AB.HI=AD.HB\)(dpcm)(1)
d,đề cứ sao sao ấy:D
`a, x^2 +6x+9 =x^2 + 2 . x . 3 +3^2 = (x+3)^2`
`b, 4x^2 +4x+1=(2x)^2 + 2 . 2x . 1+1^2=(2x+1)^2`
`c, x^2 +2xy + y^2=(x+y)^2`