
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(sinx-\sqrt{3}cos\left(x+\pi\right)=2sin2x\)
\(\Leftrightarrow sinx+\sqrt{3}cosx=2sin2x\)
\(\Leftrightarrow\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=sin2x\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x+\dfrac{\pi}{3}+k2\pi\\2x=\dfrac{2\pi}{3}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{9}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
Cả 4 đáp án đều ko đúng

1.1
\(cos2x+5sinx-3=0\)
\(\Leftrightarrow1-2sin^2x+5sinx-3=0\)
\(\Leftrightarrow2sin^2x-5sinx+2=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx=2\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)

Không thể tính được giá trị cụ thể, còn tùy thuộc hình dạng của đáy A'B'C'D'
Góc giữa A'C' và C'D' là \(\widehat{A'C'D'}\) nếu nó là góc nhọn hoặc góc bù của nó nếu nó là góc tù

5.
\(y=\dfrac{2x-1}{1-x}\Rightarrow y'=\dfrac{\left(2x-1\right)'\left(1-x\right)-\left(1-x\right)'\left(2x-1\right)}{\left(1-x\right)^2}\)
\(=\dfrac{2\left(1-x\right)+\left(2x-1\right)}{\left(1-x\right)^2}=\dfrac{1}{\left(1-x\right)^2}=\dfrac{1}{\left(x-1\right)^2}\)
9.
\(\lim\limits\dfrac{2n^2+4}{3-n^2}=\lim\dfrac{2+\dfrac{4}{n^2}}{\dfrac{3}{n^2}-1}=\dfrac{2+0}{0-1}=-2\)

3.
\(y=\dfrac{1-sin^24x}{5}=\dfrac{cos^24x}{5}\)
\(cos4x\in\left[-1;1\right]\Rightarrow cos^24x\in\left[0;1\right]\Rightarrow y\in\left[0;\dfrac{1}{5}\right]\Rightarrow\left\{{}\begin{matrix}y_{min}=0\\y_{max}=\dfrac{1}{5}\end{matrix}\right.\)
6.
\(y=sinx+cosx+2=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\)
\(sin\left(x+\dfrac{\pi}{4}\right)\in\left[-1;1\right]\Rightarrow y=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\in\left[-\sqrt{2}+2;\sqrt{2}+2\right]\)
\(\Rightarrow y_{min}=-\sqrt{2}+2\)
\(y_{max}=\sqrt{2}+2\)



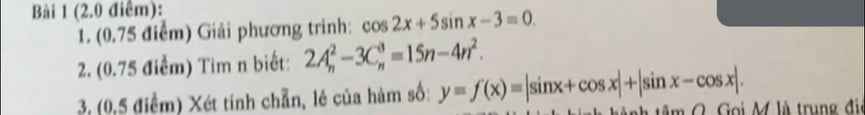







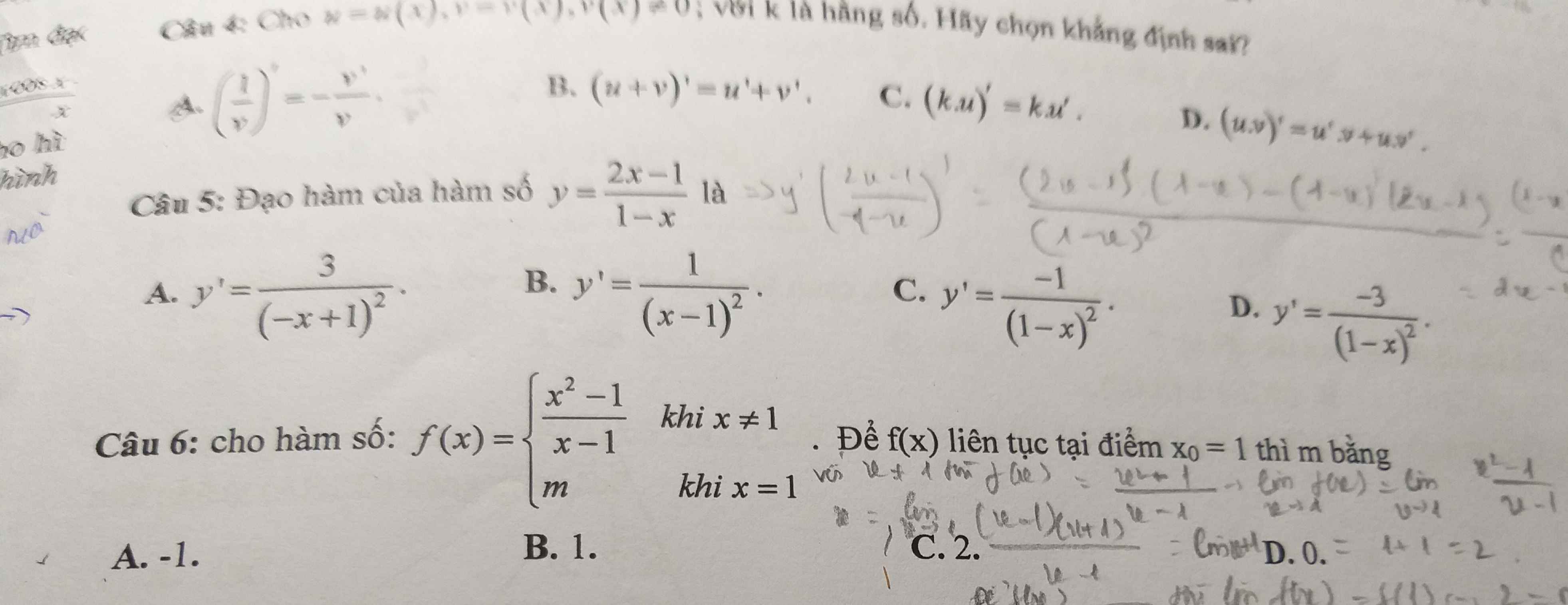


đâu
câu hỏi đâu ?????????????