
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tui làm theo cách tiểu học, để mai nghĩ xem có cách nào làm "cấp 3" ko
2+3=5; 5+3=8
Số số hạng: \(\dfrac{3n-1-2}{3}+1=n\left(so-hang\right)\)
Tổng: \(\dfrac{\left(3n-1+2\right).n}{2}=\dfrac{n\left(3n+1\right)}{2}\)

Chứng minh: 3n > 3n + 1 (1)
+ Với n = 2 thì (1) ⇔ 9 > 7 (luôn đúng).
+ Giả sử (1) đúng với n = k ≥ 2, tức là 3k > 3k + 1.
Ta chứng minh đúng với n= k+1 tức là chứng minh: 3k+ 1 > 3(k+1) + 1
Thật vậy, ta có:
3k + 1 = 3.3k > 3.(3k + 1) (Vì 3k > 3k + 1 theo giả sử)
= 9k + 3
= 3k + 3 + 6k
= 3.(k + 1) + 6k
> 3(k + 1) + 1.( vì k ≥ 2 nên 6k ≥ 12> 1)
⇒ (1) đúng với n = k + 1.
Vậy 3n > 3n + 1 đúng với mọi n ≥ 2.

Câu a làm rồi
Câu b hình như bạn nhầm đề, với dạng của dãy như vậy thì số hạng tổng quát của nó là \(n\left(3n-1\right)\) chứ ko phải \(n\left(3n+1\right)\)
\(\sum n\left(3n-1\right)=3\sum n^2-\sum n=\frac{n\left(n+1\right)\left(2n+1\right)}{2}-\frac{n\left(n+1\right)}{2}=\frac{n\left(n+1\right)}{2}\left(2n-1-1\right)=n^2\left(n+1\right)\)

tham khảo:
\(a) 2+5+8+...+(3n−1)=n(3n+1)2 (1) Đặt Sn=2+5+8+...+(3n−1) Với n=1 ta có: S1=2=1(3.1+1)2 Giả sử (1) đúng với n=k(k≥1), tức là Sk=2+5+8+...+(3k−1)=k(3k+1)2 Ta chứng minh (1) đúng với n=k+1 hay Sk+1=(k+1)(3k+4)2 Thật vậy ta có: Sk+1=2+5+8+...+(3k−1)+[3(k+1)−1]=Sk+3k+2=k(3k+1)2+3k+2=3k2+k+6k+42=3k2+7k+42=(k+1)(3k+4)2 Vậy (1) đúng với mọi k≥1 hay (1) đúng với mọi n∈N∗ b) 3+9+27+...+3n=12(3n+1−3) (2) Đặt Sn=3+9+27+...+3n=12(3n+1−3) Với n=1, ta có: S1=3=12(32−3) (hệ thức đúng) Giả sử (2) đúng với n=k(k≥1) tức là Sk=3+9+27+...+3k=12(3k+1−3) Ta chứng minh (2) đúng với n=k+1, tức là chứng minh Sk+1=12(3k+2−3) Thật vậy, ta có: Sk+1=3+9+27+...+3k+1=Sk+3k+1=12(3k+1−3)+3k+1=32.3k+1−32=12(3k+2−3)(đpcm) Vậy (2) đúng với mọi k≥1 hay đúng với mọi n∈N∗\)

a) Dễ thấy bất đẳng thức đúng với n = 2
Giả sử bất đẳng thức đúng với n = k ≥ 2, tức là
3k > 3k + 1
Nhân hai vế của (1) vơi 3, ta được:
3k + 1 > 9k + 3 <=> 3k + 1 > 3k + 4 + 6k -1.
Vì 6k - 1 > 0 nên
3k + 1 > 3k + 4 hay 3k + 1 > 3(k + 1) + 1.
tức là bất đẳng thức đúng với n = k + 1.
Vậy 3n > 3n + 1 với mọi số tự nhiên n ≥ 2.
b) Với n = 2 thì vế trái bằng 8, vế phải bằng 7. Vậy bất đẳng thức đúng với n = 2
Giả sử bất đẳng thức đúng với n = k ≥ 2, tức là
2k + 1 > 2k + 3 (2)
Ta phải chứng minh nó cũng đúng với n= k + 1, nghĩa là phải chứng minh
2k + 2 > 2(k + 1) + 3 <=> 2k + 2 > 2k + 5
Nhân hai vế của bất đẳng thức (2) với 2, ta được:
2k + 2 > 4k + 6 <=> 2k + 2 > 2k +5 + 2k + 1.
Vì 2k + 1> 0 nên 2k + 2 > 2k + 5
Vậy 2n + 1 > 2n + 3 với mọi số tự nhiên n ≥ 2.

\(\sum n\left(3n+1\right)=\sum3n^2+\sum n=3\sum n^2+\sum n\)
\(=\frac{n\left(n+1\right)\left(2n+1\right)}{2}+\frac{n\left(n+1\right)}{2}=\frac{n\left(n+1\right)}{2}\left(2n+1+1\right)=n\left(n+1\right)^2\)

a)n = 1 ⇒ 31 = 3 < 8 = 8.1
n = 2 ⇒ 32 = 9 < 16 = 8.2
n = 3 ⇒ 33 = 27 > 24 = 8.3
n = 4 ⇒ 34 = 81 > 32 = 8.4
n = 5 ⇒ 35 = 243 > 40 = 8.5
b) Dự đoán kết quả tổng quát: 3n > 8n với mọi n ≥ 3
- n = 3, bất đẳng thức đúng
- Giả sử bất đẳng thức đúng với n = k ≥ 3, nghĩa là:
3k > 8k
Ta phải chứng minh rằng bất đẳng thức cũng đúng với n = k + 1, tức là:
3(k + 1) > 8(k + 1)
Thật vậy, từ giả thiết quy nạp ta có:
3(k + 1) = 3k.3 > 8k.3 = 24k = 8k + 16k
k ≥ 3 ⇒ 16k ≥ 16.3 = 48 > 8
Suy ra: 3(k + 1) > 8k + 8 = 8(k + 1)
Vậy bất đẳng thức đúng với mọi n ≥ 3

\(=n\left(2n^2-2n-n+1\right)\)
\(=n\left(n-1\right)\left(2n-1\right)\)
TH1: n=3k
\(A=3k\left(3k-1\right)\left(6k-1\right)⋮3\)
mà A luôn chia hết cho 2(do n;n-1 là hai số liên tiếp)
nên A chia hết cho 6
TH2: n=3k+1
\(A=\left(3k+1\right)\left(3k+1-1\right)\left(6k+2-1\right)\)
\(=\left(3k+1\right)\left(3k\right)\cdot\left(6k+1\right)⋮3\)
=>A chia hết cho 6
TH3: n=3k+2
\(A=\left(3k+2\right)\left(3k+1\right)\left(6k+4-1\right)\)
\(=\left(3k+2\right)\left(3k+1\right)\left(6k+3\right)⋮6\)
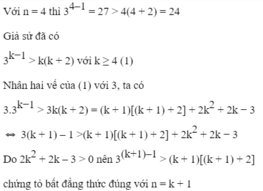
Ta có:
3n = Ba n = Bố N = Bốn = 4 .....
Vậy 3n = 4 ( với mọi n )
~ Hk T ~
3n = 4 vì:
3n hay Ba n => Bố n = 4