TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5N
1
N
16 tháng 10 2019
1.
\(DK:x\ge2\)
PT
\(\Leftrightarrow\left(2+x\right)\sqrt{x-2}-\left(x+2\right)\left(x-2\right)\)
\(\Leftrightarrow\left(x+2\right)\sqrt{x-2}\left(1-\sqrt{x-2}\right)=0\)
Cho này thì ok ròi nhé
2.
\(DK:x\le\frac{5}{2}\)
Xet \(x\in\left[0;\frac{5}{2}\right]\)
PT
\(\Leftrightarrow x^2-4x=5-2x\)
\(\Leftrightarrow x^2-2x-5=0\)
Ta co:
\(\Delta^`=\left(-1\right)^2-1.\left(-5\right)=6>0\)
\(\Rightarrow\hept{\begin{cases}x_1=1+\sqrt{6}\left(l\right)\\x_2=1-\sqrt{6}\left(l\right)\end{cases}}\)
Xet \(x\le0\)
PT
\(4x-x^2=5-2x\)
\(\Leftrightarrow x^2-6x+5=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\left(l\right)\\x=5\left(l\right)\end{cases}}\)
Vay PT vo nghiem
PK
5
TA
18 tháng 5 2021
`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)
LS
0
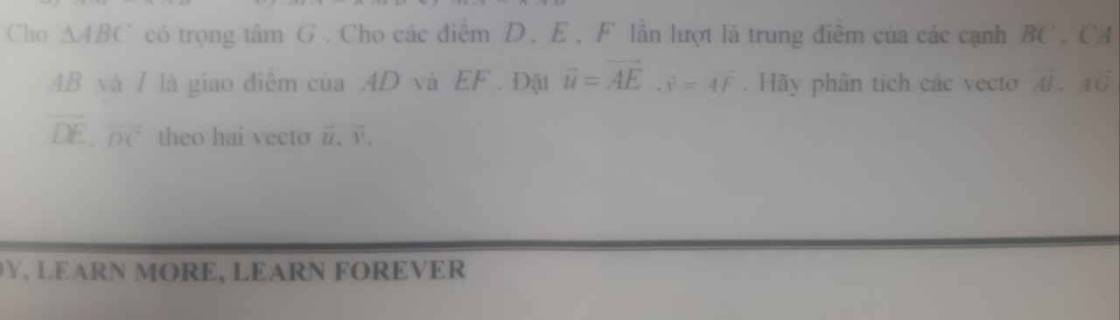
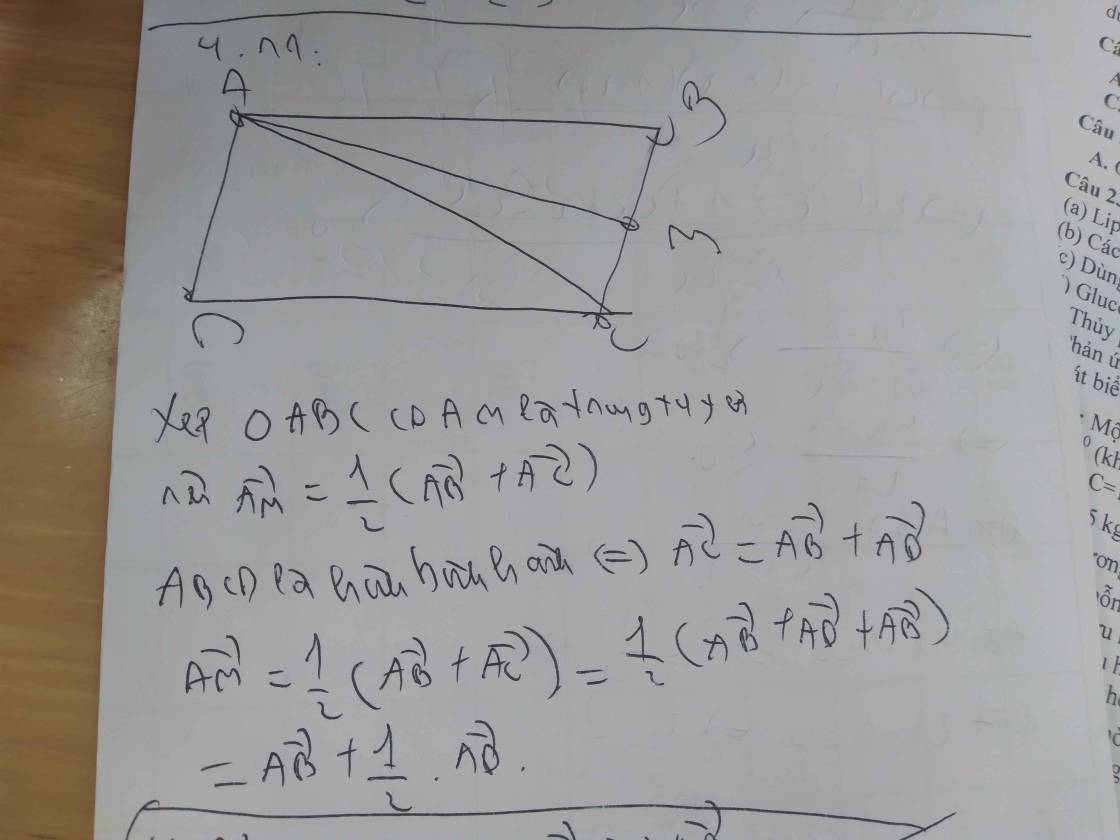
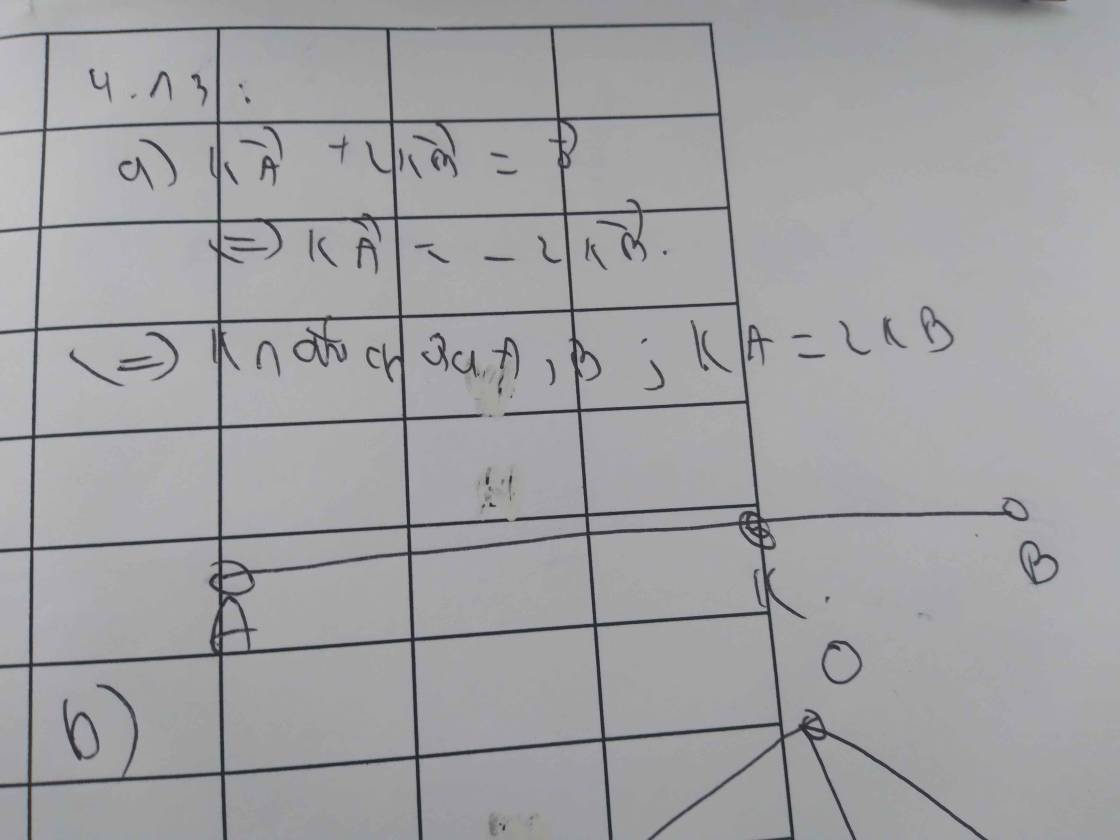
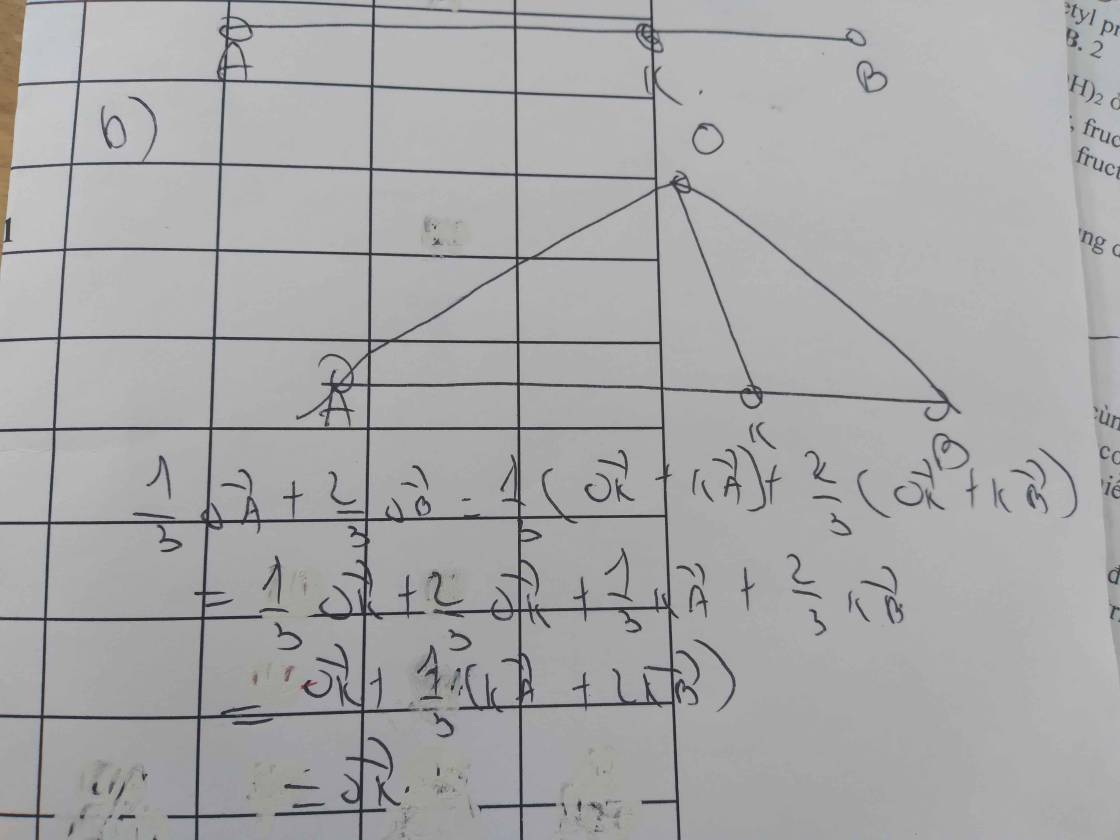
ĐKXĐ: ...
\(\Leftrightarrow\sqrt{x-1}+\sqrt{x+3}+2x+2+2\sqrt{\left(x-1\right)\left(x+3\right)}-6=0\)
Đặt \(\sqrt{x-1}+\sqrt{x+3}=t>0\)
\(\Rightarrow t^2=2x+2+2\sqrt{\left(x-1\right)\left(x+3\right)}\)
Phương trình trở thành:
\(t+t^2-6=0\Rightarrow\left[{}\begin{matrix}t=2\\t=-3\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x-1}+\sqrt{x+3}=2\)
\(\Leftrightarrow\sqrt{x-1}+\sqrt{x+3}-2=0\)
\(\Leftrightarrow\sqrt{x-1}+\dfrac{x-1}{\sqrt{x+3}+2}=0\)
\(\Leftrightarrow\sqrt{x-1}\left(1+\dfrac{\sqrt{x-1}}{\sqrt{x+3}+2}\right)=0\)
\(\Leftrightarrow\sqrt{x-1}=0\)
\(\Leftrightarrow x=1\)
Em cảm ơn thầy ạ