K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
31 tháng 10 2021
\(8,=\dfrac{13}{5}\left(\dfrac{3}{7}+\dfrac{4}{7}\right)-\dfrac{3}{5}=\dfrac{13}{5}-\dfrac{3}{5}=\dfrac{4}{5}\\ 9,=-\dfrac{5}{7}\left(\dfrac{31}{33}+\dfrac{2}{33}\right)+\dfrac{22}{17}=-\dfrac{5}{7}+\dfrac{22}{17}=\dfrac{69}{119}\\ 10,=-\dfrac{2}{15}\cdot5+\dfrac{2}{15}-\dfrac{4}{3}\cdot3=-\dfrac{2}{3}+\dfrac{2}{15}-4=-\dfrac{68}{15}\\ 11,=\dfrac{17}{3}\left(1-\dfrac{9}{17}+1-\dfrac{10}{17}\right)+\dfrac{12-25}{13}=\dfrac{17}{3}\cdot\left(2-1\right)-\dfrac{13}{13}=\dfrac{17}{3}-1=\dfrac{14}{3}\)
31 tháng 10 2021
11: \(=\dfrac{-25}{13}+\dfrac{8}{17}\cdot\dfrac{17}{3}+\dfrac{7}{17}\cdot\dfrac{17}{3}+\dfrac{12}{13}\)
\(=-1+\dfrac{8}{3}+\dfrac{7}{3}\)
=-1+5
=4
giúp mình với ạ,mình cần gấp lắm
14 tháng 1 2022
a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên DA=DE và \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE⊥BC
14 tháng 4 2021
Gọi gốc là điểm A, chỗ gãy là B, ngọn đã gãy là điểm C
Xét tam giác ABC vuông tại A có: AB = 6m, BC = 16m - 6m = 10m
=> AB2 + AC2 = BC2 (Định lý Py-ta-go)
Thay: 62 + AC2 = 102
36 + AC2 = 100
AC2 = 100 - 36 = 64
AC = 8 (m)
Vậy khoảng cách từ gốc đến ngọn cây bị gãy là 8 mét
Nếu đúng hãy K cho mình nha
Học tốt nhé
ai làm giúp mình với mình đang cần gấp lắm ạ
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 1
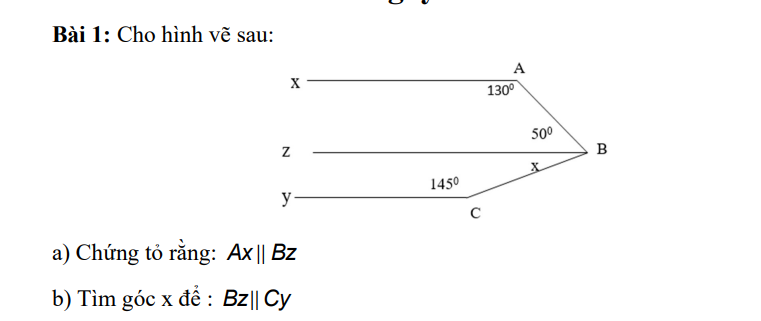
\(\widehat{XAB}\) + \(\widehat{ABZ}\) = 1300 + 500 = 1800
Vì góc XAB và góc ABZ là hai góc trong cùng phía nên
Ax // BZ
BZ // Cy ⇔ \(x\) + \(\widehat{yCB}\) =1800
⇒ \(x\) = 1800 - 1450 = 350
2D
1
15 tháng 10 2021
Bài 2:
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{45}{9}=5\)
Do đó: a=10; b=15;c=20
18 tháng 12 2021
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{1}{8}}=\dfrac{b}{\dfrac{1}{9}}=\dfrac{c}{\dfrac{1}{10}}=\dfrac{a+b+c}{\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}}=\dfrac{121}{\dfrac{121}{360}}=360\)
Do đó: a=45; b=40; c=36
H
7 tháng 5 2022
1)
- Phần hệ số: -5
- Phần biến: x3y
2)
- Để △ABC và △DEF bằng nhau thì cần thêm điều kiện BC=EF => △ABC = △DEF (cgc)
3)
a.
- Dấu hiệu ở đây là điểm kiểm tra môn Toán một tiết của mỗi học sinh lớp 7A.
-Mo=7
b.
x ̅= \(\dfrac{5.1+6.3+7.6+8.4+9.4+10.2}{20}=7.65\)
≈ 7.7 (điểm)
4)
a. A= 5x2y - 6xy - 2x2y + 6xy - 1
A= (5x2y - 2x2y) + (- 6xy + 6xy) -1
A= 3x2y -1
b. Thay x=2; y=-1 vào đa thức A có:
A = 3. 22. (-1) -1
A = 3. 4. (-1) -1
A= -12 - 1 = -13
Vậy giá trị của A tại x=2; y= -1 là -13
H
7 tháng 5 2022
5) A(x) + B(x)=(3x3- 5x2 - 2x + 13)+(-2x3 + 3x2 + 2x - 5)
= (3x3 -2x3) + (- 5x2 + 3x2) + (- 2x + 2x) + (13 – 5)
= x^3 – 2x^2 + 8
6)
Cho 3x-12=0
3x = 0 + 12 = 12
x = 12 : 3
x = 6
Vậy nghiệm của đa thức 3x – 12 = 6
7)
a. Trong △PRK, PK < PR
=> gK > gR (quan hệ giữa cạnh và góc đối diện)
b. Áp dụng định lý Py-ta-go vào △PRK có:
KR2 = PK2+ PR2
= 122 + 162
= 144 + 256 = 400
=> KR= 20 cm
8.
a.
Xét △OAC vuông tại A và △OBC vuông tại B có:
OC chung
gOAC = gOBC
=> △OAC = △OBC (ch-gn)
b.
gOAC = gOBC
=> OC là đường phân giác
=> CB = CA (tính chất tia phân giác của một góc)
Vì △OAC = △OBC nên OA = OB (2 cạnh tương ứng)
=> △OAB cân tại A
Ta có:
CB = CA => C ∈ đường trung trực của AB (1)
OA = OB => O ∈ đường trung trực của AB (2)
Từ (1) và (2) => OC là đường trung trực của AB.
9)
a. Xét △AHC và △MHC vuông tại H có:
HC chung
gACH=gMCH (HC là đường phân giác)
=> △AHC =△MHC (cgv-gn)
=> MC = AC (2 cạnh tương ứng)
=> △AMC cân tại C
b. Cho OM ⊥ AB tại O, MI ⊥ AC tại I
Xét △AMI vuông tại I và △MAK vuông tại K có:
AM cạnh chung
gMAI = AMK (tg MAC cân)
=> △AMI = △MAK (cgv-gn)
Ta thấy: \(\widehat{I}=\widehat{A}=\widehat{M}=\widehat{K}=90\) độ
=> AIMO là hình chữ nhật
=> OM = AI; OA = MI
Xét △OMA và △IAM có:
AM chung
OM = AI (cmt)
OA = MI (cmt)
=>△OMA =△IAM (ccc)
=>△OMA =△IAM = tg KMA
=> g OAM = g KAM (2 góc tương ứng)
=> AM hay AH là đường phân giác g OAK
Mặt khác: AH ⊥ EN => A
H là đường cao △ENA
AH là đường cao đồng thời là đường phân giác => △ENA cân
=> AH cũng là đường trung trực
Do đó: EH = HN nên H là trung điểm EN