
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 8:
a. Với $x,y$ là số nguyên thì $x, y-3$ cũng là số nguyên. Mà $x(y-3)=15$ nên ta có các TH:
TH1: $x=1, y-3=15\Rightarrow x=1; y=18$ (tm)
TH2: $x=-1, y-3=-15\Rightarrow x=-1; y=-12$ (tm)
TH3: $x=15; y-3=1\Rightarrow x=15; y=4$ (tm)
TH4: $x=-15; y-3=-1\Rightarrow x=-15; y=2$ (tm)
TH5: $x=3, y-3=5\Rightarrow x=3; y=8$ (tm)
TH6: $x=-3; y-3=-5\Rightarrow x=-3; y=-2$ (tm)
TH7: $x=5; y-3=3\Rightarrow x=5; y=6$ (tm)
TH8: $x=-5; y-3=-3\Rightarrow x=-5; y=0$ (tm)
Câu 8:
b.
$xy-2y+3(x-2)=7$
$\Rightarrow y(x-2)+3(x-2)=7$
$\Rightarrow (x-2)(y+3)=7$
Do $x,y$ nguyên nên $x-2, y+3$ nguyên. Mà tích của chúng bằng $7$ nên ta có các TH sau:
TH1: $x-2=1, y+3=7\Rightarrow x=3; y=4$ (tm)
TH2: $x-2=-1; y+3=-7\Rightarrow x=1; y=-10$ (tm)
TH3: $x-2=7, y+3=1\Rightarrow x=9; y=-2$ (tm)
TH4: $x-2=-7; y+3=-1\Rightarrow x=-5; y=-4$ (tm)

Các số được điền vào các ô theo thứ tự từ trái sang phải là:
-1; - \(\dfrac{1}{3}\); \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)

1)
a. Xét tg ABC cân tại A có AC=AB; gACB = g ABC.
Xét tg ACN và tg ABM có:
CN=BM (gt)
AC=AB
gACB=gABC
=> tg ACN = tg ABM (cgc)
=> AN=AM (2 cạnh tg ứng)
H là trung điểm BC nên AH là đường trung tuyến của tg ABC
Mak tg ABC cân => H cũng là đường cao của tg ABC => AH ⊥ BC
b. Vì H là trung đ của BC nên CH=HB=BC/2= 3cm
Áp dụng định lý Py ta go vào tg AHB có:
AB^2=AH^2+HB^2
AH^2= AB^2 - HB^2
AH^2= 5^2 - 3^2 = 16 cm
=> AH= 4 cm
c. Xét tg AMN và tg KMB có:
AM=KM (gt)
MN=BM (gt)
gHMA=gKMB (đối đỉnh)
=> tg AMN = tg KMB (cgc)
d. tg AMN = tg KMB => gMAN=gMKB
=> AN=KB=Am
Mà AB>AM (quan hệ giữ đường xiêng và hình chiếu) nên AB>BK
=> gBKA> gBAK
=> gMAN>gBAM

=)) Mik chịu á, bạn cứ làm mấy chỗ khác trước và chừa chứng minh cho mik cx đc ạ

b: \(\sqrt{8^2+6^2}-\sqrt{16}+\dfrac{1}{2}\sqrt{\dfrac{4}{25}}\)
\(=10-4+\dfrac{1}{2}\cdot\dfrac{2}{5}=6+\dfrac{1}{5}=\dfrac{31}{5}\)



1) \(\left(\dfrac{-13}{17}-\dfrac{31}{52}\right)-\left(\dfrac{73}{52}-\dfrac{13}{17}+\dfrac{5}{6}\right)-\dfrac{3}{4}\)
\(=\dfrac{-13}{17}-\dfrac{31}{52}-\dfrac{73}{52}+\dfrac{13}{17}-\dfrac{5}{6}-\dfrac{3}{4}\)
\(=\left(\dfrac{-13}{17}+\dfrac{13}{17}\right)-\left(\dfrac{31}{52}+\dfrac{73}{52}\right)-\left(\dfrac{5}{6}+\dfrac{3}{4}\right)\)
\(=0-2-\dfrac{19}{12}\)
\(=-2-\dfrac{19}{12}\)
\(=\dfrac{-43}{12}\)



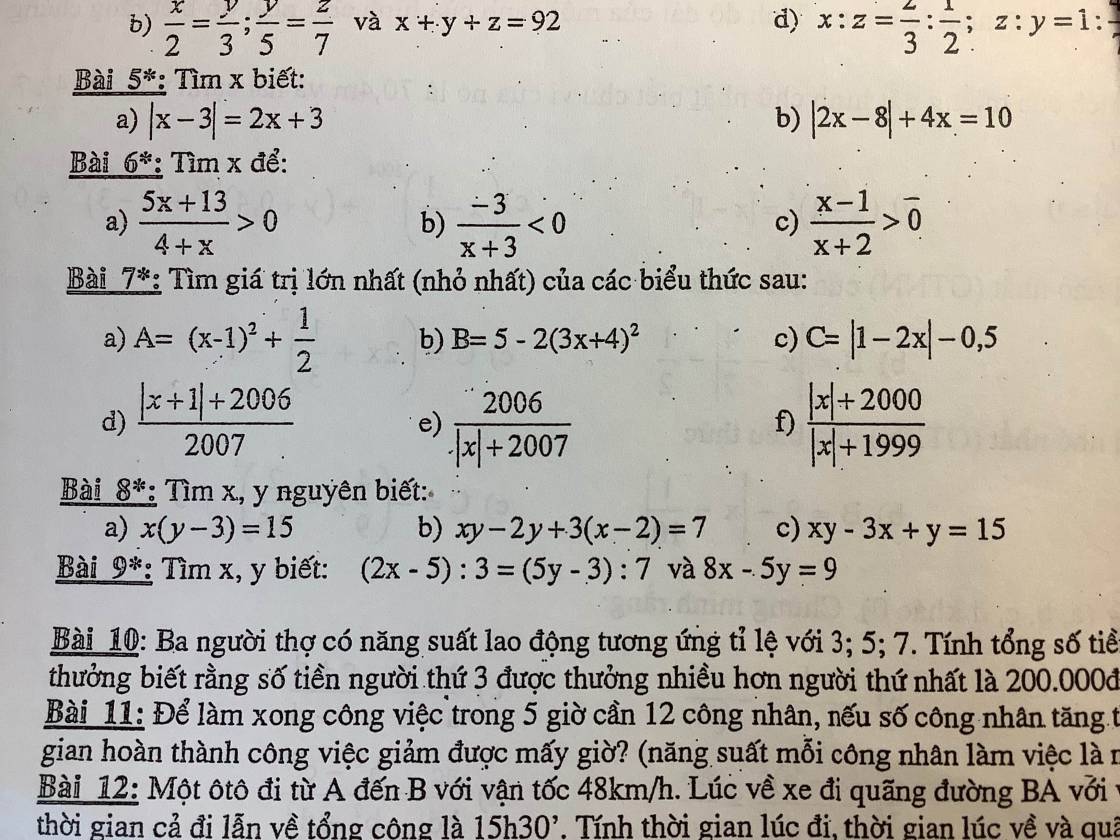


 Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn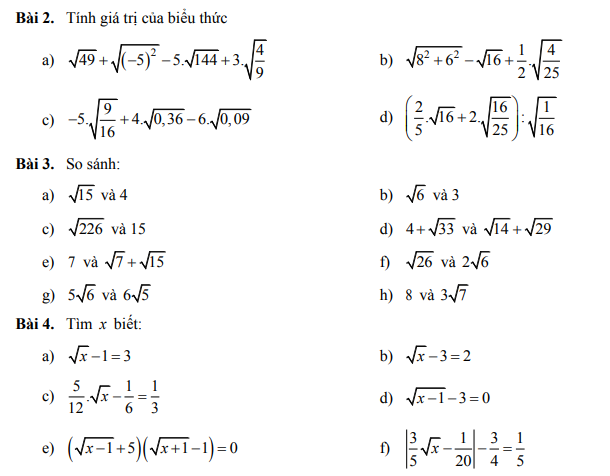 các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy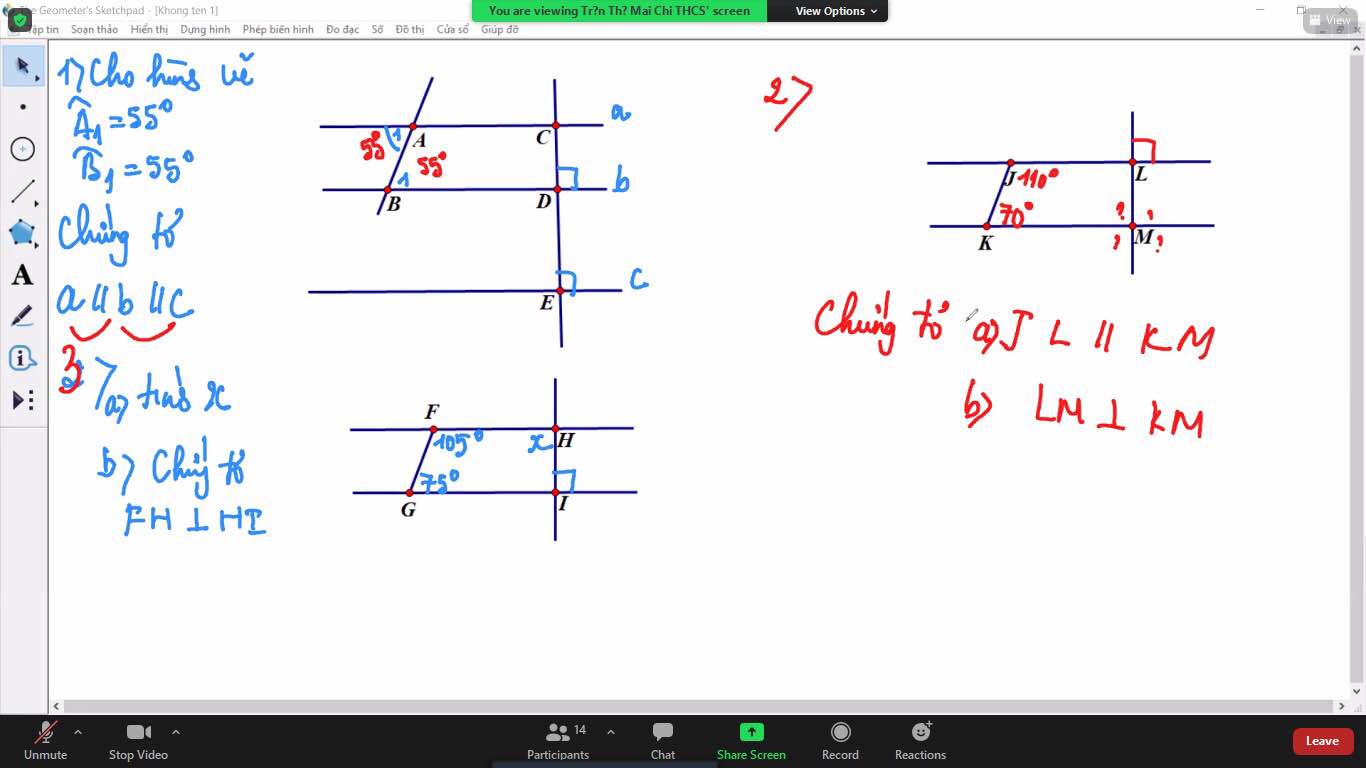


2) So sánh:
a) \(3^{24}=\left(3^6\right)^4=729^4< 3125^4=\left(5^5\right)^4=5^{20}\)
c) \(\left(\frac{1}{2}\right)^{300}=\left(\frac{1}{2^3}\right)^{100}=\left(\frac{1}{8}\right)^{100}>\left(\frac{1}{9}\right)^{100}=\left(\frac{1}{3^2}\right)^{100}=\left(\frac{1}{3}\right)^{200}\)
b) \(17^{20}=\left(17^4\right)^5>\left(3^4\right)^5=81^5>71^5\)
d) \(\left(\frac{1}{3}\right)^{75}=\left(\frac{1}{3^3}\right)^{25}=\left(\frac{1}{27}\right)^{25}< \left(\frac{1}{25}\right)^{25}=\left(\frac{1}{5^2}\right)^{25}=\left(\frac{1}{5}\right)^{50}\)
e) \(2^{27}=\left(2^3\right)^9=8^9< 9^9=\left(3^2\right)^9=3^{18}\)
g) \(32^9=\left(2^5\right)^9=2^{45}=2^{13}.2^{32}=2^{13}.\left(2^4\right)^8=2^{13}.16^8< 2^{13}.27^8=2^{13}.3^{24}\)
\(< 2^{13}.3^{26}=\left(2.3^2\right)^{13}=18^{13}\)
3) Tìm \(x\), biết:
a) \(\left(\frac{3}{4}\right)^x=\frac{2^8}{3^4}\)
\(\Leftrightarrow\left(\frac{3}{4}\right)^x=\left(\frac{4}{3}\right)^4\)
\(\Leftrightarrow\left(\frac{3}{4}\right)^x=\left(\frac{3}{4}\right)^{-4}\)
\(\Leftrightarrow x=-4\)
b) \(\left(x-2\right)^8=\left(x-2\right)^6\)
\(\Leftrightarrow\left(x-2\right)^6\left[\left(x-2\right)^2-1\right]=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\\left(x-2\right)^2=1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=3,x=1\end{cases}}\).
c) \(\left(1,78^{2x-2}-1,78^x\right)\div1,78^x=0\)
\(\Leftrightarrow1,78^{x-2}-1=0\)
\(\Leftrightarrow1,78^{x-2}=1,78^0\)
\(\Leftrightarrow x-2=0\)
\(\Leftrightarrow x=2\).
d) \(5^{\left(x-2\right)\left(x+3\right)}=1\)
\(\Leftrightarrow\left(x-2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x+3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=-3\end{cases}}\)
e) \(2021^{x^2+3x-4}=1\)
\(\Leftrightarrow x^2+3x-4=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+4=0\\x-1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-4\\x=1\end{cases}}\)