K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 10 2019
Đề thế này hả bạn: \(2sin\frac{5x}{2}.sin\frac{x}{2}-mcosx+1=0\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 9 2020
\(\Leftrightarrow4cos^3x-3cosx-\left(2cos^2x-1\right)+m.cosx-1=0\)
\(\Leftrightarrow4cos^3x-2cos^2x+\left(m-3\right)cosx=0\)
\(\Leftrightarrow cosx\left(4cos^2x-2cosx+m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\left(1\right)\\4cos^2x-2cosx+m-3=0\left(2\right)\end{matrix}\right.\)
Xét (1) \(\Rightarrow x=\frac{\pi}{2}+k\pi\) không có nghiệm nào trên khoảng đã cho
\(\Rightarrow\) (2) phải có 7 nghiệm trên khoảng đã cho
Mà (2) là pt bậc 2 nên có tối đa 2 nghiệm cosx, ứng với mỗi giá trị cosx cũng có tối đa 2 nghiệm x thuộc khoảng đã cho
\(\Rightarrow\) (2) có tối đa 4 nghiệm
Không tồn tại m thỏa mãn yêu cầu
NV
0
CM
6 tháng 7 2019
Chọn A.
y' = (m + 1)cosx – msinx – ( m + 2)
Phương trình y’ = 0 ⇔ (m + 1)cosx – msinx = (m + 2)
Điều kiện phương trình có nghiệm là a2 + b2 ≥ c2
⇔ (m + 1)2 + m2 ≥ (m + 2)2 ⇔ m2 – 2m – 3 ≥ 0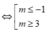 
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2023
\(y'=\left(m+1\right)cosx-msinx-\left(m+2\right)\)
\(y'=0\Rightarrow\left(m+1\right)cosx-msinx=m+2\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất, pt đã cho có nghiệm khi:
\(\left(m+1\right)^2+m^2\ge\left(m+2\right)^2\)
\(\Leftrightarrow m^2-2m-3\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-1\end{matrix}\right.\)
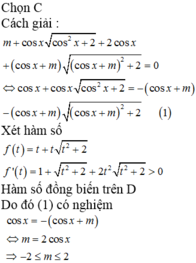
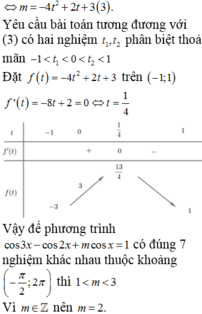
huhuh giúp mk vs mn ơi