
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
a: =>3x=24
hay x=8
b: =>5x-2x=-11+3
=>3x=-8
hay x=-8/3
c: =>4/3x=17
hay x=51/4
d: =>3/7x=-8
hay x=-56/3

a.\(A=\dfrac{1}{x-1}-\dfrac{x^2+x}{x^2+1}.\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\);\(ĐK:x\ne\pm1\)
\(A=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\left(\dfrac{x+1-x+1}{\left(x-1\right)\left(x+1\right)}\right)\)
\(A=\dfrac{1}{\left(x-1\right)}-\dfrac{2x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)\left(x^2+1\right)}\)
\(A=\dfrac{1}{x-1}-\dfrac{2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{x^2+1-2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{x-1}{x^2+1}\)
b.\(A=0,2=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{x-1}{x^2+1}=\dfrac{1}{5}\)
\(\Leftrightarrow x^2+1=5x-5\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
c.\(A< 0\) mà \(x^2+1\ge1>0\)
--> A<0 khi \(x-1< 0\)
\(\Leftrightarrow x< 1\)
a. -ĐKXĐ:\(x\ne\pm1\)
\(A=\dfrac{1}{x-1}-\dfrac{x^2+x}{x^2+1}.\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\left(\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}-\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\dfrac{x+1-x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\dfrac{2}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}\)
\(=\dfrac{x^2+1}{\left(x^2+1\right)\left(x-1\right)}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}\)
\(=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\)
b. \(A=\dfrac{x-1}{x^2+1}=0,2\)
\(\Leftrightarrow\dfrac{x-1}{x^2+1}=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{5\left(x-1\right)}{5\left(x^2+1\right)}=\dfrac{x^2+1}{5\left(x^2+1\right)}\)
\(\Rightarrow5x-5=x^2+1\)
\(\Leftrightarrow x^2-5x+1+5=0\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow x^2-2x-3x+6=0\)
\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=3\left(nhận\right)\end{matrix}\right.\)
c. \(A=\dfrac{x-1}{x^2+1}< 0\)
\(\Leftrightarrow x-1< 0\) (vì \(x^2+1>0\forall x\))
\(\Leftrightarrow x< 1\)

2:
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>DE=AH=12cm
b: ΔAHB vuông tại H có HD vuông góc AB
nên AD*AB=AH^2
ΔAHC vuông tại H có HE vuông góc AC
nên AE*AC=AH^2
=>AD*AB=AE*AC
c: góc IAC+góc AED
=góc ICA+góc AHD
=góc ACB+góc ABC=90 độ
=>AI vuông góc ED
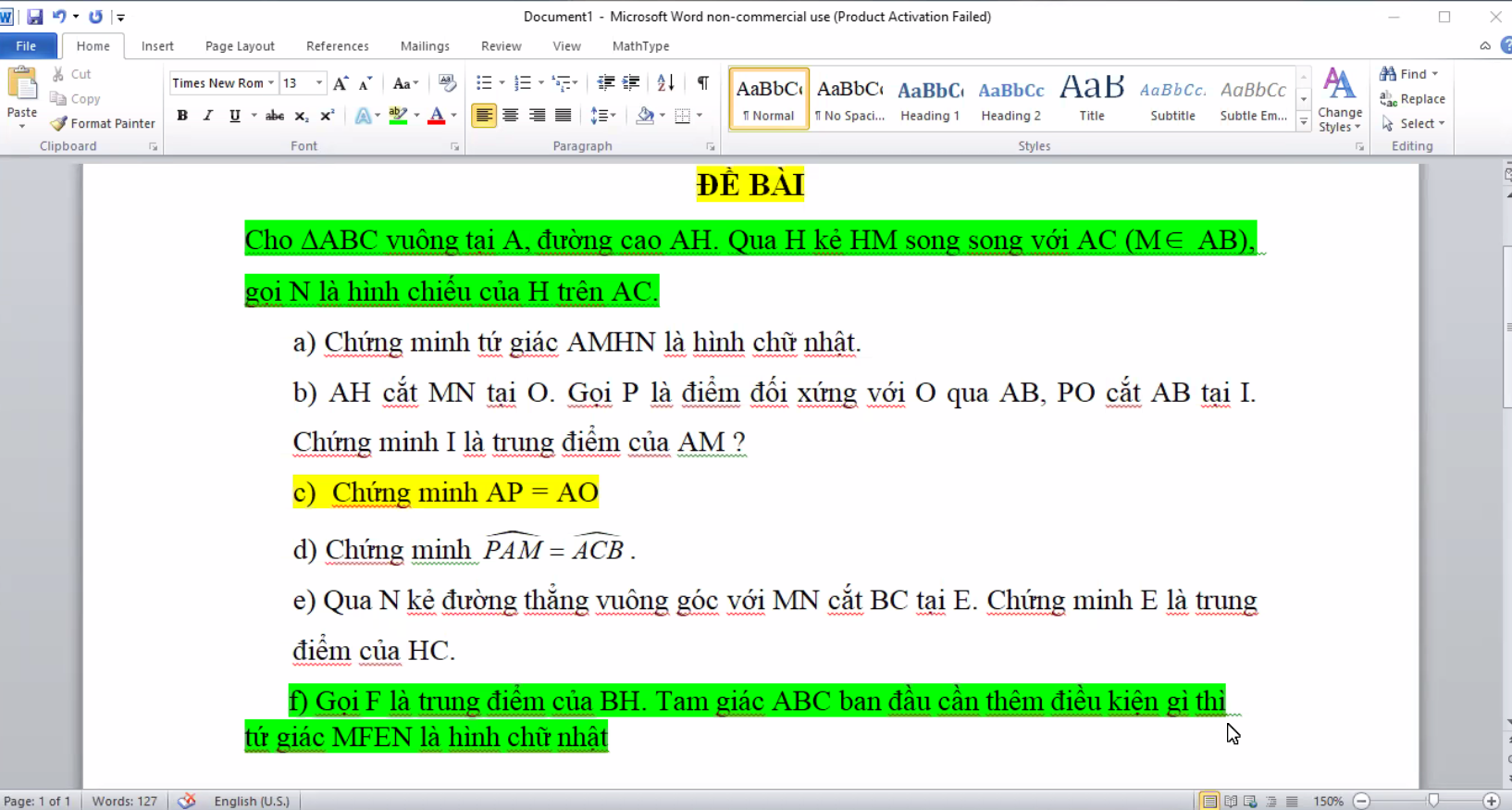
4:
a: góc BDH=góc BEH=góc DBE=90 độ
=>BDHE là hình chữ nhật
b: BDHE là hình chữ nhật
=>góc BED=góc BHD=góc A
Xét ΔBED và ΔBAC có
góc BED=góc A
góc EBD chung
=>ΔBED đồng dạng với ΔBAC
=>BE/BA=BD/BC
=>BE*BC=BA*BD
c: góc MBC+góc BED
=góc C+góc BHD
=góc C+góc A=90 độ
=>BM vuông góc ED

đặt M là n^3 -9n^2+2n.
TH1 : n có dạng 2k => M chia hết cho 2 (bạn tự cm)
TH2 ; n có dạng 2k+1 => M = (2k+1)^3-9(2k+1)^2+2n
=8k^3+6k+12k^2+1-9(4k^2+4k+1)+2n = ... => M chia hết cho 2 với mọi n (1)
Xét n có dạng 3k => M chia hết cho 3
Xét n có dạng 3k+1 => n^3+2n=(3k+1)^3+2(3k+1)=27k^3+9k+27k^2+6k+3 chia hết cho 3 mà 9n^2 cũng chia hết cho 3 => M chia hết cho 3
Tương tự bạn xét n =3k+2....
=> M chia hết cho 3 vs mọi n (2)
Từ (1) và (2) => M chia hết cho 6


Bài 1:
a) \(5x^2y-10xy^2=5xy\left(x-y\right)\)
b) \(4x\left(2y-z\right)+7y\left(z-2y\right)=\left(4x-7y\right)\left(2y-z\right)\)
c) \(5x^2y^3-25x^3y^4+10x^3y^3=5x^2y^3\left(1-5xy+2x\right)\)
d) \(12x^2y-18xy^2-30y^2=6y\left(2x^2-3xy-5y\right)\)
e) \(y\left(a-b\right)-7y^2\left(b-a\right)=\left(y+7y^2\right)\left(a-b\right)\)
f) \(27x^2\left(y-1\right)-9x^3\left(1-y\right)=\left(27x^2+9x^3\right)\left(y-1\right)=9x^2\left(3+x\right)\left(y-1\right)\)

bài 1
a)
=(x+y-x+y)(x+y+x-y)
=2x.2y
=4xy
b)
B=(x+y-x+y)2=4y2
c)
=(x+y-x+y)[(x+y)2+(x+y)(x-y)+(x-y)2]-2y3
=2y(\(x^2+2xy+y^2+x^2-y^2+x^2-2xy+y^2\))-2y3
=\(2y\left(3x^2+y^2\right)-2y^3=6x^2y+2y^3-2y^3=6x^2y\)
Bài 3:
a: Ta có: \(A=\left(x+y\right)^2-\left(x-y\right)^2\)
\(=x^2+2xy+y^2-x^2+2xy-y^2\)
=4xy
b: ta có: \(B=\left(a+b\right)^3+\left(a-b\right)^3-2a^3\)
\(=a^3+3a^2b+3ab^2+b^3+a^3-3a^2b+3ab^2-b^3-2a^3\)
\(=6ab^2\)
c: Ta có: \(C=9^8\cdot2^8-\left(18^4-1\right)\left(18^4+1\right)\)
\(=18^8-18^8+1\)
=1


Gọi vận tốc thực là x
Độ dài quãng đường AB là 4(x+2)
Theo đề, ta có phươg trình:
4(x+2)=5(x-2)
=>5x-10=4x+8
=>x=18
Vậy: Độ dài quãng đường là 80km

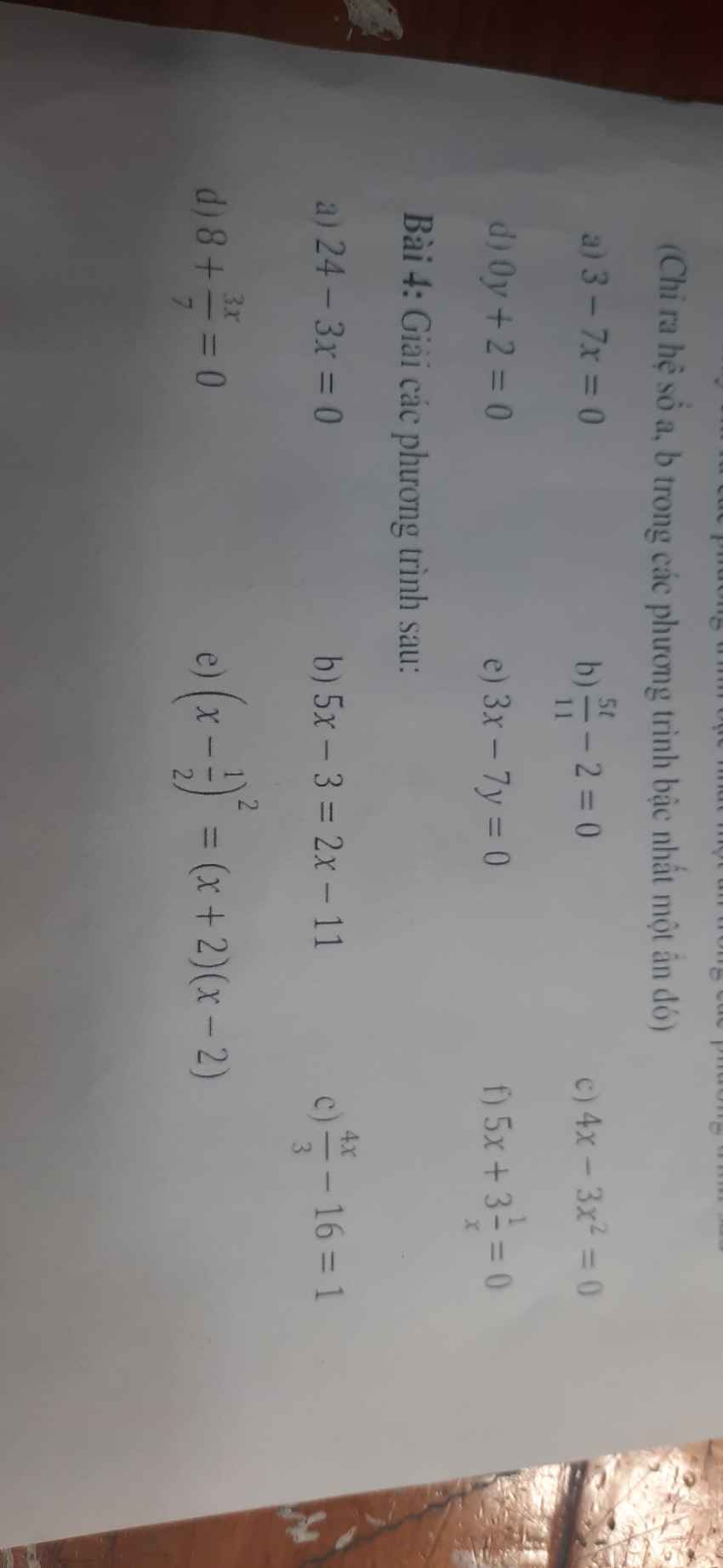
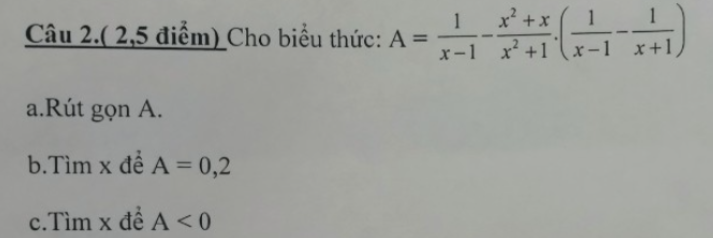

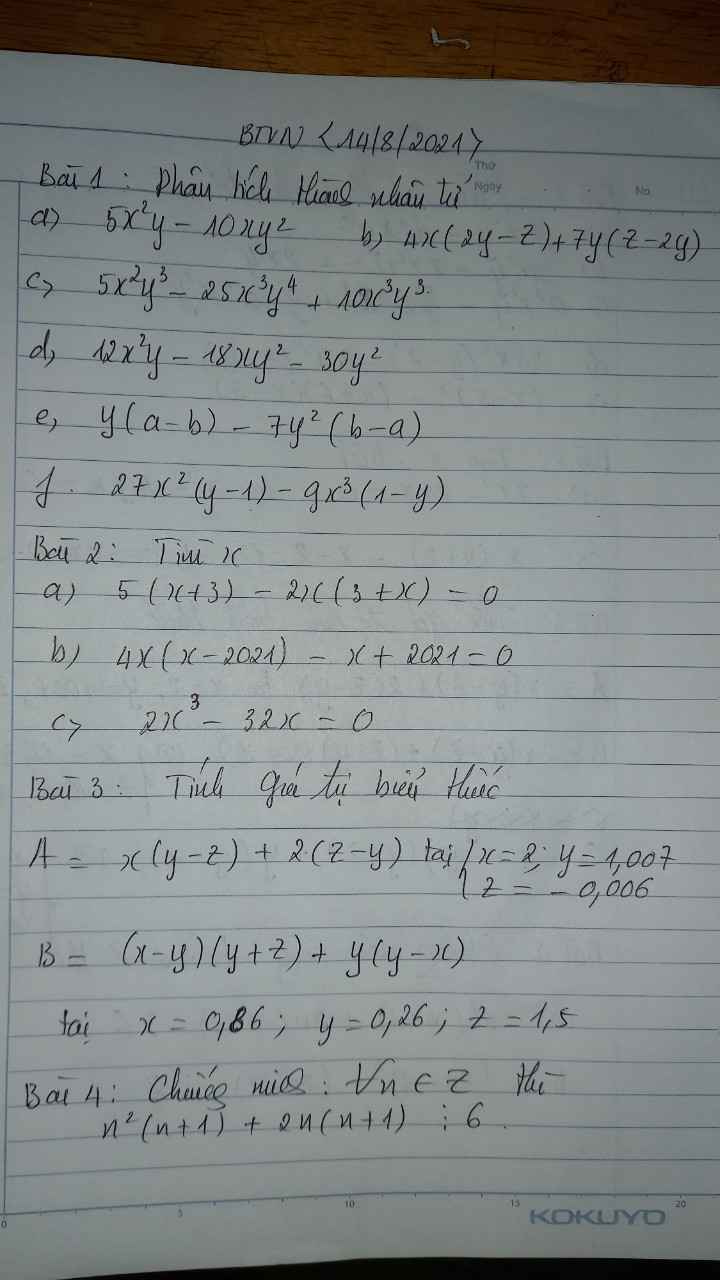 lm giúp mik vs
lm giúp mik vs 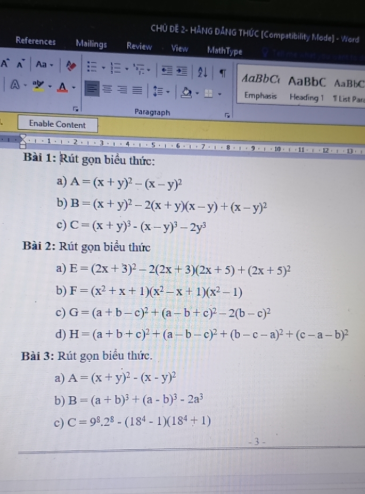 lm giúp mik vs
lm giúp mik vs 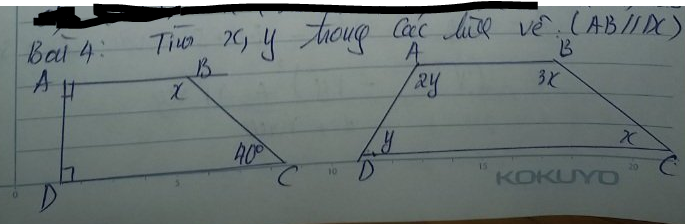 lm giúp mik vs
lm giúp mik vs 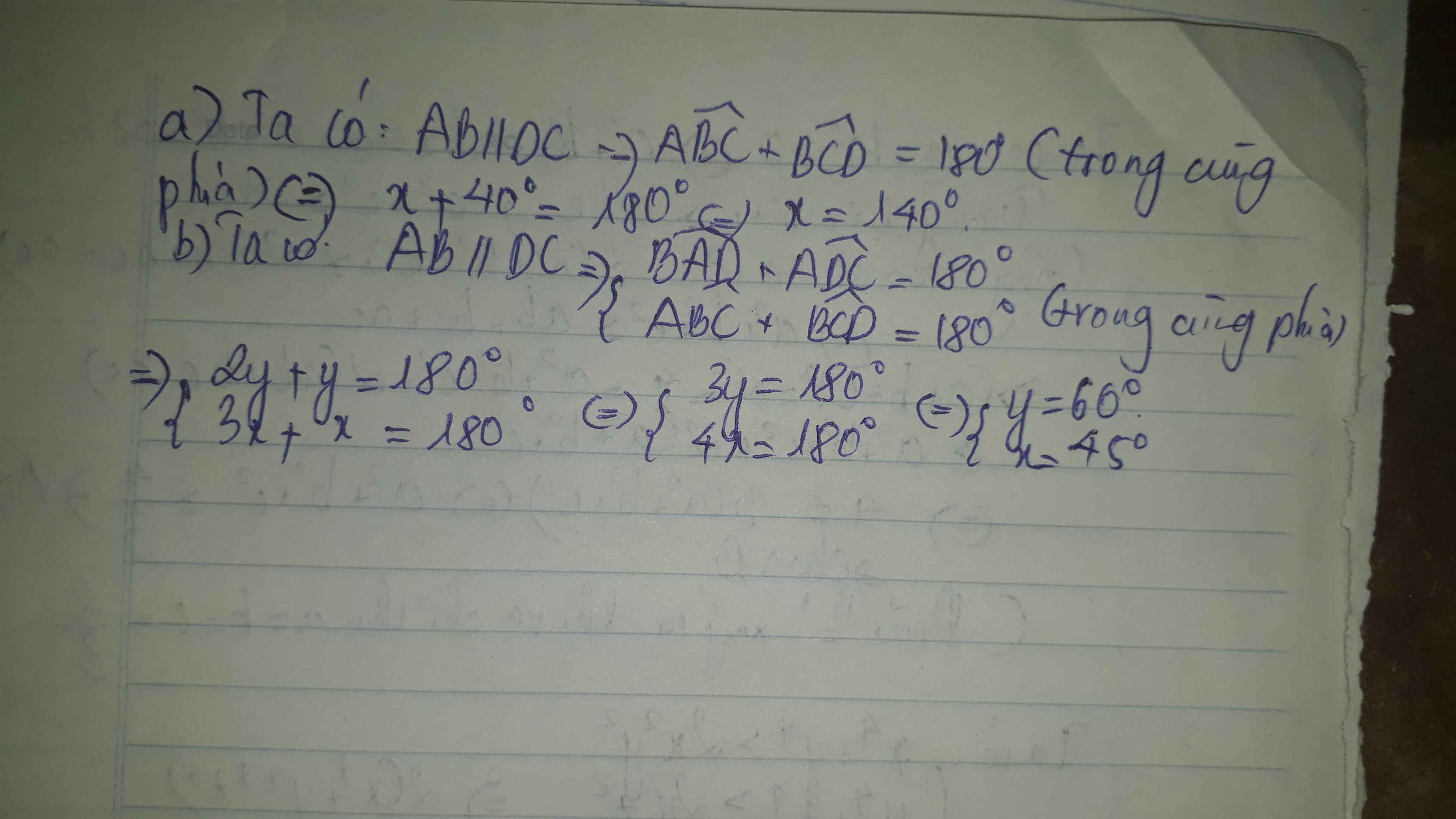
Với |x| = 2 khi x = 2 hoặc x = -2
a, \(A=\left(3x+5\right)\left(2x-1\right)+\left(4x-1\right)\left(3x+2\right)\)
\(=6x^2+7x-5+12x^2+5x-2=18x^2+12x-7\)
Với x = 2 thì \(A=89\)
Với x = -2 thì \(A=41\)
b, \(B=\left(x^3-x^2y+xy^2-y^3\right)\left(x+y\right)\)
\(=x^4+x^3y-x^3y-x^2y^2+x^2y^2+xy^3-xy^3-y^4=x^4-y^4\)
Thay x = 2 ; y = -1/4 ta được : \(=16-\frac{1}{256}=\frac{4095}{256}\)
Bài 4 :
a, \(3\left(1-4x\right)\left(x-1\right)+4\left(3x-2\right)\left(x+3\right)=-27\)
\(\Leftrightarrow3\left(x-1-4x^2+4x\right)+4\left(3x^2+7x-6\right)=-27\)
\(\Leftrightarrow-12x^2+15x-3+12x^2+28x-24=-27\)
\(\Leftrightarrow43x=0\Leftrightarrow x=0\)
b, \(\left(2x+3\right)\left(x-4\right)+\left(x-5\right)\left(x-2\right)=\left(3x-5\right)\left(x-4\right)\)
\(\Leftrightarrow2x^2-5x-12+x^2-7x+10=3x^2-17x+20\)
\(\Leftrightarrow-12x-2=-17x+20\Leftrightarrow5x=22\Leftrightarrow x=\frac{22}{5}\)