
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

Bài 1:
a.
$a^3-a^2c+a^2b-abc=a^2(a-c)+ab(a-c)$
$=(a-c)(a^2+ab)=(a-c)a(a+b)=a(a-c)(a+b)$
b.
$(x^2+1)^2-4x^2=(x^2+1)^2-(2x)^2=(x^2+1-2x)(x^2+1+2x)$
$=(x-1)^2(x+1)^2$
c.
$x^2-10x-9y^2+25=(x^2-10x+25)-9y^2$
$=(x-5)^2-(3y)^2=(x-5-3y)(x-5+3y)$
d.
$4x^2-36x+56=4(x^2-9x+14)=4(x^2-2x-7x+14)$
$=4[x(x-2)-7(x-2)]=4(x-2)(x-7)$
Bài 2:
a. $(3x+4)^2-(3x-1)(3x+1)=49$
$\Leftrightarrow (3x+4)^2-[(3x)^2-1]=49$
$\Leftrightarrow (3x+4)^2-(3x)^2=48$
$\Leftrightarrow (3x+4-3x)(3x+4+3x)=48$
$\Leftrightarrow 4(6x+4)=48$
$\Leftrightarrow 6x+4=12$
$\Leftrightarrow 6x=8$
$\Leftrightarrow x=\frac{4}{3}$
b. $x^2-4x+4=9(x-2)$
$\Leftrightarrow (x-2)^2=9(x-2)$
$\Leftrightarrow (x-2)(x-2-9)=0$
$\Leftrightarrow (x-2)(x-11)=0$
$\Leftrightarrow x-2=0$ hoặc $x-11=0$
$\Leftrightarrow x=2$ hoặc $x=11$
c.
$x^2-25=3x-15$
$\Leftrightarrow (x-5)(x+5)=3(x-5)$
$\Leftrightarrow (x-5)(x+5-3)=0$
$\Leftrightarrow (x-5)(x+2)=0$
$\Leftrightarrow x-5=0$ hoặc $x+2=0$
$\Leftrightarrow x=5$ hoặc $x=-2$

Xét tứ giác ABEC có
AB//EC
AC//BE
Do đó: ABEC là hình bình hành
Suy ra: AC=BE
mà AC=BD
nên BE=BD
hay ΔBED cân tại B

Câu 4:
a: ĐKXĐ: \(x\notin\left\{0;-5\right\}\)
b: \(A=\dfrac{x^2+2x}{2\left(x+5\right)}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2}{2x\left(x+5\right)}+\dfrac{2\left(x^2-25\right)}{2x\left(x+5\right)}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+4x^2-5x}{2x\left(x+5\right)}=\dfrac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}\)
\(=\dfrac{x\left(x+5\right)\left(x-1\right)}{2x\left(x+5\right)}=\dfrac{x-1}{2}\)
c: Để A=-3 thì x-1=-6
hay x=-5(loại)


52 + 122 =132 => tg vuong
Sabc = 12.5/2 = 30cm2
( toán violympic cho rất thông minh, mới nhìn là mk phát hiện ra r , thui mk đi học đây)
Tam giác ABC có 3 cạnh của tam giác ứng với định lí Py-ta-go=> ABC là tam giác vuông
\(S_{ABC}=\frac{5.12}{2}=30cm^2\)


a)tam giác BHA có BI là phân giác(góc ABI=góc HBI) nên \(\dfrac{AI}{IH}=\dfrac{AB}{BH}\Rightarrow AI\cdot BH=AB\cdot IH\)
b)xét tam giác BHA và tam giác BAC có:
góc ABC chung
góc BHA=góc BAC=90 độ
\(\Rightarrow\Delta BHA\infty\Delta BAC\left(g.g\right)\\ \Rightarrow\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow AB^2=BH\cdot BC\)
c)ta có:
theo câu a) \(\dfrac{AI}{IH}=\dfrac{AB}{BH}\Rightarrow\dfrac{IH}{AI}=\dfrac{BH}{AB}\left(1\right)\)
theo câu b) \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\)
ta lại có BD là phân giác góc ABC nên \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{AD}{DC}=\dfrac{BH}{AB}\)(2)
từ (1) và (2)\(\Rightarrow\dfrac{IH}{IA}=\dfrac{AD}{DC}\left(=\dfrac{BH}{AB}\right)\)
 lm giúp mik vs
lm giúp mik vs 



 giúp mk nha mờn nhìu ạk
giúp mk nha mờn nhìu ạk









 Mọi Người giải giúp em ạ em cảm ơn ạ
Mọi Người giải giúp em ạ em cảm ơn ạ  giúp mik với nha!
giúp mik với nha! cac
cac
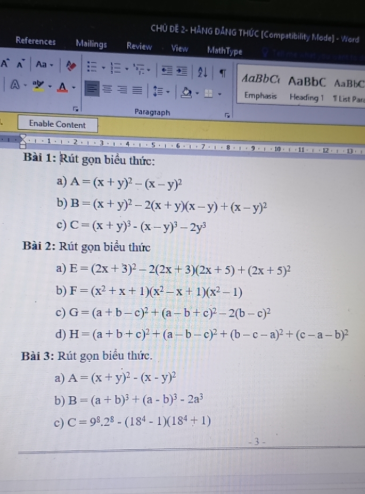
bài 1
a)
=(x+y-x+y)(x+y+x-y)
=2x.2y
=4xy
b)
B=(x+y-x+y)2=4y2
c)
=(x+y-x+y)[(x+y)2+(x+y)(x-y)+(x-y)2]-2y3
=2y(\(x^2+2xy+y^2+x^2-y^2+x^2-2xy+y^2\))-2y3
=\(2y\left(3x^2+y^2\right)-2y^3=6x^2y+2y^3-2y^3=6x^2y\)
Bài 3:
a: Ta có: \(A=\left(x+y\right)^2-\left(x-y\right)^2\)
\(=x^2+2xy+y^2-x^2+2xy-y^2\)
=4xy
b: ta có: \(B=\left(a+b\right)^3+\left(a-b\right)^3-2a^3\)
\(=a^3+3a^2b+3ab^2+b^3+a^3-3a^2b+3ab^2-b^3-2a^3\)
\(=6ab^2\)
c: Ta có: \(C=9^8\cdot2^8-\left(18^4-1\right)\left(18^4+1\right)\)
\(=18^8-18^8+1\)
=1