
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x-7\right)^{x+1}-\left(x-7\right)^{x+11}=0\)
\(\Rightarrow\left(x-7\right)^{x+1}\left[1-\left(x-7\right)^{10}\right]=0\)
\(\Rightarrow\left(x-7\right)^{x+1}\left[1^2-\left(x-7\right)^{5^2}\right]=0\)
\(\Rightarrow\left(x-7\right)^{x+1}\left[1-\left(x-7\right)^5\right]\left[1+\left(x-7\right)^5\right]=0\)
=>(x-7)x+1=0 hoặc 1-(x-7)5=0 hoặc 1+(x-7)5=0
+)Nếu (x-7)x+1=0
=>x-7=0
=>x=7
+)Nếu 1-(x-7)5=0
=>(x-7)5=1
=>x-7=1
=>x=8
+)Nếu 1+(x-7)5=0
=>(x-7)5=-1
Vì \(\left(x-7\right)^5\ge0\) với mọi x
=>không tìm được x thỏa mãn 1+(x-7)5=0
Vậy x=7 hoặc x=8

a) \(\frac{1}{4}+\frac{1}{3}\div\left(2x-1\right)=-5\)
\(\Leftrightarrow\frac{1}{3}\div\left(2x-1\right)=-5-\frac{1}{4}\)
\(\Leftrightarrow\frac{1}{3}\div\left(2x-1\right)=\frac{-20}{4}-\frac{1}{4}\)
\(\Leftrightarrow\frac{1}{3}\div\left(2x-1\right)=\frac{-21}{4}\)
\(\Leftrightarrow\left(2x-1\right)=\frac{1}{3}\div\frac{-21}{4}\)
\(\Leftrightarrow\left(2x-1\right)=\frac{-4}{63}\)
\(\Leftrightarrow2x=\frac{-4}{63}+1\)
\(\Leftrightarrow2x=\frac{-4}{63}+\frac{63}{63}\)
\(\Leftrightarrow2x=\frac{59}{63}\)
\(\Leftrightarrow x=\frac{59}{63}\div2\)
\(\Leftrightarrow x=\frac{59}{126}\)
b) \(-\left(5\frac{3}{8}+x-7\frac{5}{24}\right)\div2019\frac{11}{37}=0\)
\(\Leftrightarrow-\left(5\frac{3}{8}+x-7\frac{5}{24}\right)=0.2019\frac{11}{37}\)
\(\Leftrightarrow-5\frac{3}{8}-x+7\frac{5}{24}=0\)
\(\Leftrightarrow\frac{-43}{8}-x+\frac{173}{24}=0\)
\(\Leftrightarrow\frac{-129}{24}-x+\frac{173}{24}=0\)
\(\Leftrightarrow-x+\frac{44}{24}=0\)
\(\Leftrightarrow x=\frac{44}{24}-0\)
\(\Leftrightarrow x=\frac{44}{24}=\frac{11}{6}\)


\(a)\) \(\left(2x+1\right)\left(2x-3\right)=7\)
Có \(4\) trường hợp :
\(\Leftrightarrow\)\(\hept{\begin{cases}2x+1=1\\2x-3=7\end{cases}\Leftrightarrow\hept{\begin{cases}2x=0\\2x=10\end{cases}\Leftrightarrow}\hept{\begin{cases}x=0\\x=5\end{cases}}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}2x+1=-1\\2x-3=-7\end{cases}\Leftrightarrow\hept{\begin{cases}2x=-2\\2x=-4\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-1\\x=-2\end{cases}}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}2x+1=7\\2x-3=1\end{cases}\Leftrightarrow\hept{\begin{cases}2x=6\\2x=4\end{cases}\Leftrightarrow}\hept{\begin{cases}x=3\\x=2\end{cases}}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}2x+1=-7\\2x-3=-1\end{cases}\Leftrightarrow\hept{\begin{cases}2x=-8\\2x=2\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-4\\x=1\end{cases}}}\)
Vậy không có giá trị nào của x thoả mãn đề bài
\(b)\) \(x\left(x-7\right)+3\left(x-7\right)=11\)
\(\Leftrightarrow\)\(\left(x+3\right)\left(x-7\right)=11\)
Có \(4\) trường hợp :
\(\Leftrightarrow\)\(\hept{\begin{cases}x+3=1\\x-7=11\end{cases}\Leftrightarrow\hept{\begin{cases}x=-2\\x=18\end{cases}}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}x+3=-1\\x-7=-11\end{cases}\Leftrightarrow\hept{\begin{cases}x=-4\\x=-4\end{cases}}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}x+3=11\\x-7=1\end{cases}\Leftrightarrow\hept{\begin{cases}x=8\\x=8\end{cases}}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}x+3=-11\\x-7=-1\end{cases}\Leftrightarrow\hept{\begin{cases}x=-14\\x=6\end{cases}}}\)
Vậy \(x\in\left\{-4;8\right\}\)

a: (x+1/2)(2/3-2x)=0
=>x+1/2=0 hoặc 2/3-2x=0
=>x=-1/2 hoặc x=1/3
b: 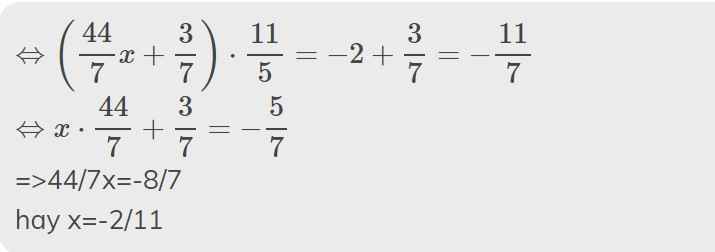
c: \(\Leftrightarrow x\cdot\left(\dfrac{13}{4}-\dfrac{7}{6}\right)=\dfrac{5}{12}+\dfrac{5}{3}=\dfrac{5}{12}+\dfrac{20}{12}=\dfrac{25}{12}\)
\(\Leftrightarrow x=\dfrac{25}{12}:\dfrac{39-14}{12}=\dfrac{25}{25}=1\)

\(y+30\%y=-1,3\\ 130\%y=-1,3\\ \Rightarrow y=\dfrac{-1,3}{130\%}=-1\)
\(x:\dfrac{4}{28}=\dfrac{13}{-19}+\dfrac{8}{25}\\ 7x=-\dfrac{173}{475}\\ x=-\dfrac{\dfrac{173}{475}}{7}=-\dfrac{173}{3325}\)
\(\left(x-7\right)^{x+1}-\left(x-7\right)^{x+11}=0\)
\(\Rightarrow\left(x-7\right)^{x+1}\left[1-\left(x-7\right)^{10}\right]=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-7\right)^{x+1}=0\\1-\left(x-7\right)^{10}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=7\\\left[{}\begin{matrix}x-7=-1\\x-7=1\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=7\\x=6\\x=8\end{matrix}\right.\)
Vậy x = 7 hoặc x = 6 hoặc x = 8
\(\left(x-7\right)^{x+1}-\left(x-7\right)^{x+11}=0\\ \left(x-7\right)^{x+1}\left[1-\left(x-7\right)^{10}\right]=0\\ \Rightarrow\left[{}\begin{matrix}\left(x-7\right)^{x+1}=0\\1-\left(x-7\right)^{10}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x-7=0\\x-7=\pm1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=7\\x=\pm1+7\end{matrix}\right.\)
vậy x={6;7;8}