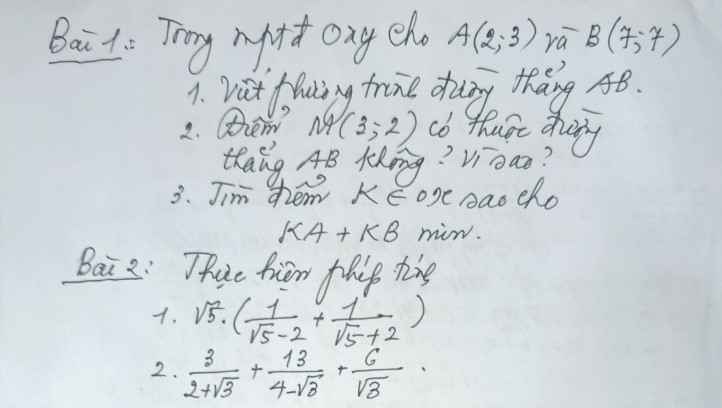Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để hệ có nghiệm duy nhất thì \(\dfrac{a}{1}\ne\dfrac{2a}{a+1}\)
=>\(a\left(a+1\right)\ne2a\)
=>\(a^2+a-2a\ne0\)
=>\(a^2-a\ne0\)
=>\(a\left(a-1\right)\ne0\)
=>\(a\notin\left\{0;1\right\}\)

a. Bạn tự giải.
b.
\(\left\{{}\begin{matrix}ax-2y=a\\-4x+2y=2a+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}ax-2y=a\\\left(a-4\right)x=3a+2\end{matrix}\right.\)
Hệ có nghiệm duy nhất khi \(a-4\ne0\Leftrightarrow a\ne4\)
Khi đó: \(\left\{{}\begin{matrix}x=\dfrac{3a+2}{a-4}\\y=\dfrac{a^2+3a}{a-4}\end{matrix}\right.\)
\(x-y=1\Leftrightarrow\dfrac{3a+2}{a-4}-\dfrac{a^2+3a}{a-4}=1\)
\(\Leftrightarrow\dfrac{2-a^2}{a-4}=1\Leftrightarrow2-a^2=a-4\)
\(\Leftrightarrow a^2+a-6=0\Rightarrow\left[{}\begin{matrix}a=2\\a=-3\end{matrix}\right.\)

a) Ta có: \(\left\{{}\begin{matrix}x+my=2\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}mx+m^2y=2m\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2y+2y=2m-1\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y\left(m^2+2\right)=2m-1\\mx=1+2y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2m-1}{m^2+2}\\x=\dfrac{1+2y}{m}=\left(1+\dfrac{2m-1}{m^2+2}\right)\cdot\dfrac{1}{m}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2+2+2m-1}{m^2+2}\cdot\dfrac{1}{m}=\dfrac{m^2+2m+1}{m\left(m^2+2\right)}\\y=\dfrac{2m-1}{m^2+2}\end{matrix}\right.\)
Để hệ phương trình có nghiệm duy nhất thỏa mãn x>0 và y>0 thì \(\left\{{}\begin{matrix}\dfrac{m^2+2m+1}{m\left(m^2+2\right)}>0\\\dfrac{2m-1}{m^2+2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\2m-1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\m>\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow m>\dfrac{1}{2}>0\)
Vậy: Khi m>0 thì hệ phương trình có nghiệm duy nhất (x,y) thỏa mãn x>0 và y>0

Vì \(\dfrac{3}{1}\ne\dfrac{-1}{2}\)
nên hệ luôn có nghiệm duy nhất
\(\left\{{}\begin{matrix}3x-y=2m-1\\x+2y=3m+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-y=2m-1\\3x+6y=9m+6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-7y=2m-1-9m-6=-7m-7\\x+2y=3m+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=m+1\\x=3m+2-2m-2=m\end{matrix}\right.\)
\(y-\sqrt{x}=1\)
=>\(m+1-\sqrt{m}=1\)
=>\(m-\sqrt{m}=0\)
=>\(\sqrt{m}\left(\sqrt{m}-1\right)=0\)
=>\(\left[{}\begin{matrix}m=0\\m=1\end{matrix}\right.\)

\(\left\{{}\begin{matrix}2x-y=m+1\\x+y=2m-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=3m\\2x-y=m+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m\\y=m-1\end{matrix}\right.\)
Theo đề: \(x^2-2y-1=0\)
\(\Leftrightarrow m^2-2\left(m-1\right)-1=0\)
\(\Leftrightarrow m^2-2m+1=0\)
\(\Leftrightarrow\left(m-1\right)^2=0\Leftrightarrow m=1\).
Vậy: \(m=1.\)

\(HPT\Leftrightarrow\left\{{}\begin{matrix}x=m-y\\m-y+ym+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m-y\\ym=1-m\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=m-\dfrac{1-m}{m}=\dfrac{m^2+m-1}{m}\\y=\dfrac{1-m}{m}\end{matrix}\right.\)
\(x+2y>0\\ \Leftrightarrow\dfrac{m^2+m-1}{m}+\dfrac{2-2m}{m}>0\\ \Leftrightarrow\dfrac{m^2-m+1}{m}>0\)
Mà \(m^2-m+1=\left(m-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
Vậy \(m>0\) thỏa đề