K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
26 tháng 5 2019
Gọi giao điểm AO với BC là H.
ΔAHB và ΔAHC có:
cạnh AH chung,
AB = AC
∠(BAH) = ∠(CAH) (theo b).
⇒ ΔAHB = ΔAHC (c.g.c)
⇒ HB = HC và ∠(AHB) = ∠(AHC)
Lại có: ∠(AHB) + ∠(AHC) = 180º ( hai góc kề bù)
Suy ra: ∠(AHB) = ∠(AHC) = 90º
tức là AO ⊥ BC và AO đi qua trung điểm của BC.

18 tháng 5 2022
a: Xét ΔPBC và ΔQCB có
PB=QC
\(\widehat{PBC}=\widehat{QCB}\)
BC chung
Do đo: ΔPBC=ΔQCB
Suy ra: \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
b: OB=OC
AB=AC
Do đó: AO là đường trung trực của BC
Ta có: ΔABC cân tại A
mà AO là đường trung trực
nên AO là đường phân giác
hay O cách đều hai cạnh AB và AC
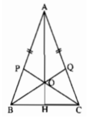
The two triangles BAP and BAO have the same height from B, so we have: \(\dfrac{S_{BAP}}{S_{BAO}}=\dfrac{AP}{AO}\)
Similarly, we have: \(\dfrac{S_{CAP}}{S_{CAO}}=\dfrac{AP}{AO}\), from that, we have: \(\dfrac{AP}{AO}=\dfrac{S_{BAP}}{S_{BAO}}=\dfrac{S_{CAP}}{S_{CAO}}=\dfrac{S_{BAP}+S_{CAP}}{S_{BAO}+S_{CAO}}=\dfrac{S_{ABC}}{S_{BAO}+S_{CAO}}\)
Thus, we also have \(\dfrac{BQ}{OB}=\dfrac{S_{ABC}}{S_{BOC}+S_{AOB}}\); \(\dfrac{CR}{OC}=\dfrac{S_{ABC}}{S_{BOC}+S_{AOC}}\)
So we get: \(\dfrac{AP}{AO}+\dfrac{BQ}{OB}+\dfrac{CR}{OC}=\dfrac{S_{ABC}}{S_{COA}+S_{AOB}}+\dfrac{S_{ABC}}{S_{AOB}+S_{BOC}}\)\(+\dfrac{S_{ABC}}{S_{BOC}+S_{AOC}}\)
If \(S_{BOC}=a;S_{COA}=b;S_{AOB}=c\left(a,b,c>0\right)\), then \(P=\dfrac{AP}{AO}+\dfrac{BQ}{OB}+\dfrac{CR}{OC}=\dfrac{S_{ABC}}{b+c}+\dfrac{S_{ABC}}{c+a}+\dfrac{S_{ABC}}{a+b}\)
\(=S_{ABC}\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\right)\)
We have already had the inequality: \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\ge\dfrac{9}{x+y+z}\) (This is true with all of the positive real number \(x,y,z\). If you don't know about this, please check it on the Internet) \(P\ge S_{ABC}\left(\dfrac{9}{a+b+b+c+c+a}\right)=S_{ABC}.\dfrac{9}{2\left(a+b+c\right)}\)\(=S_{ABC}.\dfrac{9}{2S_{ABC}}=\dfrac{9}{2}\) (vì \(a+b+c=S_{BOC}+S_{COA}+S_{AOB}=S_{ABC}\))
In conclusion, the minimum value of \(\dfrac{AP}{AO}+\dfrac{BQ}{OB}+\dfrac{CR}{OC}\) is \(\dfrac{9}{2}\), happens when \(a=b=c=\dfrac{1}{3}S_{ABC}\) or \(S_{BOC}=S_{COA}=S_{AOC}=\dfrac{1}{3}S_{ABC}\)
Consider \(S_{BOC}=\dfrac{1}{3}S_{ABC}\Leftrightarrow\dfrac{S_{BOC}}{S_{ABC}}=\dfrac{1}{3}\)
We have \(\dfrac{S_{BOP}}{S_{ABP}}=\dfrac{PO}{PA}\) and \(\dfrac{S_{COP}}{S_{ACP}}=\dfrac{PO}{PA}\)
Therefore, we have \(\dfrac{PO}{PA}=\dfrac{S_{BOP}}{S_{ABP}}=\dfrac{S_{COP}}{S_{ACP}}=\dfrac{S_{BOP}+S_{COP}}{S_{ABP}+S_{ACP}}=\dfrac{S_{BOC}}{S_{ABC}}=\dfrac{1}{3}\)
Similarly, we have \(\dfrac{OQ}{BQ}=\dfrac{1}{3};\dfrac{OR}{CR}=\dfrac{1}{3}\)
These means O is the centroid of the triangle ABC.
So in order to minimize the value of \(\dfrac{AP}{AO}+\dfrac{BQ}{OB}+\dfrac{CR}{OC}\), O must be the centroid of the triangle ABC.