Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔPBC và ΔQCB có
PB=QC
\(\widehat{PBC}=\widehat{QCB}\)
BC chung
Do đo: ΔPBC=ΔQCB
Suy ra: \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
b: OB=OC
AB=AC
Do đó: AO là đường trung trực của BC
Ta có: ΔABC cân tại A
mà AO là đường trung trực
nên AO là đường phân giác
hay O cách đều hai cạnh AB và AC

ΔOBC cân tại O ⇒ OB = OC.
ΔAOB và ΔAOC có: AO chung, AB = AC (giả thiết), OB = OC (cmt)
⇒ ΔAOB = ΔAOC (c.c.c).
⇒ ∠BAO = ∠CAO
⇒ AO là tia phân giác của góc BAC
⇒ O cách đều hai cạnh AB, AC

Ta sẽ chứng minh ΔOBC có hai góc OBC và OCB bằng nhau
ΔABQ và ΔACP có: AB = AC, AQ = AP, ∠A chung
⇒ ΔABQ = ΔACP (c.g.c)
⇒ ∠ABQ = ∠ACP.
Mà ∠ABC = ∠ACB (Vì tam giác ABC cân tại A)
⇒ ∠ABC - ∠ABQ = ∠ACB - ∠ACP hay ∠OBC = ∠OCB
⇒ ΔOBC cân tại O.

a: Xét ΔPBC và ΔQCB có
PB=QC
góc PBC=góc QCB
BC chung
Do đó: ΔPBC=ΔQCB
Suy ra: \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
b: Kẻ OH vuông góc với AB,OK vuông góc với AC
Xét ΔOHB vuông tại H và ΔOKC vuông tại K có
OB=OC
\(\widehat{OBH}=\widehat{OCK}\)
Do đó: ΔOHB=ΔOKC
Suy ra: OH=OK
c: Ta có: AB=AC
OB=OC
Do đó:AO là đường trung trực của BC
=>AO vuông góc với BC tại trung điểm của BC
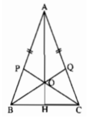
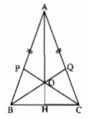
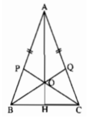
Gọi giao điểm AO với BC là H.
ΔAHB và ΔAHC có:
cạnh AH chung,
AB = AC
∠(BAH) = ∠(CAH) (theo b).
⇒ ΔAHB = ΔAHC (c.g.c)
⇒ HB = HC và ∠(AHB) = ∠(AHC)
Lại có: ∠(AHB) + ∠(AHC) = 180º ( hai góc kề bù)
Suy ra: ∠(AHB) = ∠(AHC) = 90º
tức là AO ⊥ BC và AO đi qua trung điểm của BC.