Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số tam giác lập được là: \(C^2_6\cdot1=15\left(tamgiác\right)\)

Đáp án: B
a, b đúng.
c sai vì Góc tạo bởi hai tia phân giác của hai góc kề bù là góc vuông không phải góc nhọn.
d sai vì Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến dường thẳng đó, đường vuông góc là đường ngắn nhất không phải dài nhất.

(C): x^2+y^2+4x-2y-4=0
=>(x+2)^2+(y-1)^2=9
=>I(-2;1); R=3
M thuộc d nên M(a;1-a)
M nằm ngoài (C) nên IM>R
=>IM^2>9
=>2a^2+4a-5>0
MA^2=MB^2=IM^2-IA^2=(a+2)^2+(-a)^2-9=2a^2+4a-5
=>x^2+y^2-2ax+2(a-1)y-6a+6=0(1)
A,B thuộc (C)
=>Tọa độ A,B thỏa mãn phương trình:
x^2+y^2+4x-2y-4=0(2)
(1)-(2)=(a+2)x-ay+3a-5=0(3)
Tọa độ A,B thỏa mãn (3) nên (3) chính là phương trình đường thẳng AB
(E) tiếp xúc AB nên (E): R1=d(E,AB)
Chu vi của (E) lớn nhất khi R1 lớn nhất
=>d(E;AB) lớn nhất
Gọi H là hình chiếu vuông góc của E lên AB
=>d(E,Δ)=EH<=EK=căn 10/2
Dấu = xảy ra khi H trùng K
=>AB vuông góc EK
vecto EK=(-1/2;3/2), AB có VTCP là (a;a+2)
AB vuông góc EK
=>-1/2a+3/2(a+2)=0
=>a=-3
=>M(-3;4)

Cách 1:
TH1: 2 điểm thuộc a và 1 điểm thuộc b
Số cách chọn 2 điểm thuộc đường thẳng a là \(C_3^2\) (cách chọn)
Số cách chọn 1 điểm thuộc đường thẳng b là: \(C_4^1\) (cách chọn)
=> Số tam giác tạo thành là: \(C_3^2 . C_4^1 = 12\)
TH2: 2 điểm thuộc b và 1 điểm thuộc a
Số cách chọn 2 điểm thuộc đường thẳng b là \(C_4^2\) (cách chọn)
Số cách chọn 1 điểm thuộc đường thẳng a là: \(C_3^1\) (cách chọn)
=> Số tam giác tạo thành là: \(C_4^2 + C_3^1 = 18\)
Vậy có tất cả 12 + 18 = 30 tam giác.
Cách 2:
Số cách chọn 3 điểm thuộc đường thẳng a là: \(C_3^3\) (cách chọn)
Số cách chọn 3 điểm thuộc đường thẳng b là: \(C_4^3\) (cách chọn)
Số cách chọn 3 điểm bất kì trong 7 điểm đã cho là: \(C_7^3\) (cách chọn)
Số cách chọn 3 điểm không thẳng hàng trong 7 điểm đã cho là: \(C_7^3 - C_4^3 - C_3^3 = 30\) (cách chọn)
Vậy số tam giác có thể có là : 30 (tam giác)

Khi ba điểm M, N, P thẳng hàng, trong đó điểm N nằm giữa hai điểm M và P. Khi đó, M N → ; M P → cùng hướng với nhau.
Đáp án B

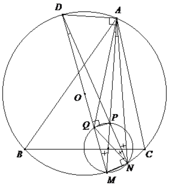
1). Vì MP là đường kính suy ra P N ⊥ M N (1).
Vì MD là đường kính suy ra D N ⊥ M N (2).
Từ (1) và (2), suy ra N; P; D thẳng hàng.