K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HL
1
CM
28 tháng 8 2017
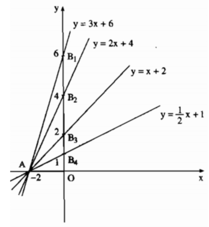
Gọi ∠ ( B 1 Ax) = α 1 ; ∠ ( B 2 Ax) = α 2 ; ∠ ( B 3 Ax) = α 3 ; ∠ ( B 4 Ax) = α 4 . Dùng máy tính bỏ túi CASIO fx – 220 tính tg α 1 , tg α 2 , tg α 3 , tg α 4 và suy ra các góc tương ứng.
Ta có:
tg α 1 = 3 ⇒ α 1 ≈ 71 ° 33 ' 54 , 18 ' '
tg α 2 = 2 ⇒ α 2 ≈ 63 ° 26 ' 5 , 82 ' '
tg α 3 = 1 ⇒ α 3 ≈ 45 °
tg α 4 = 1/2 ⇒ α 4 ≈ 26 ° 33 ' 54 , 18 ' '
20 tháng 9 2016
\(f\left(a,b\right)=a^2+8b^2-6ab+14a-40b+48=3\)
\(\Leftrightarrow f\left(a,b\right)=a^2+8b^2-6ab+14a-40b+45=0\)
\(\Leftrightarrow a^2+2a\left(7-3b\right)+\left(8b^2-40b+45\right)=0\)
Xét \(\Delta'=\left(7-3b\right)^2-\left(8b^2-40b+45\right)=b^2-2b+4=\left(b-1\right)^2+3>0\)
Vậy PT luôn có hai nghiệm phân biệt.
Vì a,b nguyên nên \(b^2-2b+4=k^2\left(k\in N\right)\)
\(\Leftrightarrow k^2-\left(b-1\right)^2=3\Leftrightarrow\left(k-b+1\right)\left(k+b-1\right)=3\)
Xét các trường hợp với k-b+1 và k+b-1 là các số nguyên được :
(b;k) = (0;2) ; (0;-2) ; (2;2) ; (2;-2)
Thay lần lượt các giá trị của b vào f(a,b) = 3 để tìm a.
Vậy : (a;b) = (-9;0) ; (-5;0) ; (-3;2) ; (1;2)
26 tháng 7 2017
Đặt \(\sqrt{x^2+x+0,1}=a\ge0\) cho dễ nhìn
\(\Rightarrow\sqrt{2009+2010a}-\sqrt{2009-2010a}=20\)\(\left(0\le a\le\frac{2009}{2010}\right)\)
\(\Leftrightarrow2009+2009-2\sqrt{2009^2-2010^2a^2}=400\)
\(\Leftrightarrow\sqrt{2009^2-2010^2a^2}=1809\)
\(\Leftrightarrow2009^2-2010^2a^2=1809^2\)
\(\Leftrightarrow a^2=\frac{7636}{40401}\)
\(\Rightarrow x^2+x+0,1=\frac{7636}{40401}\)
Đây là phương trình bậc 2 nên bấm máy tính giải nghiệm đi nha.