Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì đường thẳng \(d:y = mx\) đi qua các điểm \(A;B;C;D;E;F\) nên ta chọn \(A\left( {20;10} \right)\) thay vào đường thẳng ta được:
\(10 = 20.m \Leftrightarrow m = 10:20 \Leftrightarrow m = \dfrac{1}{2}\)
Do đó đường thẳng cần tìm là: \(y = \dfrac{1}{2}x\).
Hệ số góc của đường thẳng là \(a = \dfrac{1}{2}\).

a) Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2; - 6} \right);\left( { - 1; - 3} \right);\left( {0;0} \right);\left( {1;3} \right);\left( {2;6} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây
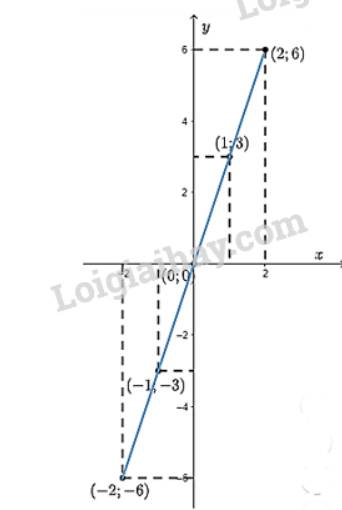
b) Các điểm vừa xác định được ở câu a đều nằm trên một đường thẳng.

Đồ thị hàm số là tập hợp các điểm có tọa độ \(A\left( {18;36} \right);B\left( {20;40} \right);C\left( {21;42} \right);\) \(D\left( {25;50} \right);\)\(E\left( {28;56} \right);\)\(F\left( {30;60} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây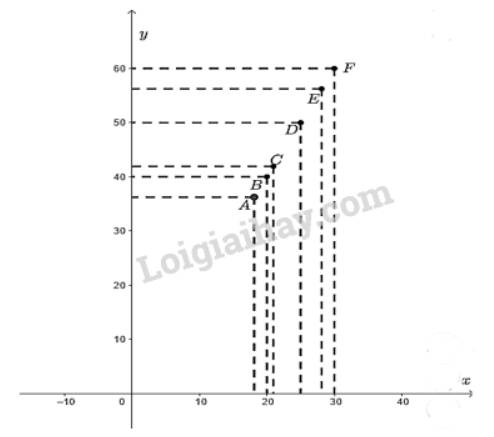

a) Đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ xác nhận được duy nhất một giá trị \(y\) tương ứng.
b) \(f\left( 2 \right) = {2^2} = 4;f\left( { - 3} \right) = {\left( { - 3} \right)^2} = 9\)
Ta có: \(f\left( { - 2} \right) = {\left( { - 2} \right)^2} = 4;f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\(f\left( 0 \right) = {0^2} = 0;f\left( 1 \right) = {1^2} = 1\)
\(f\left( 2 \right) = {2^2} = 4;f\left( 3 \right) = {3^2} = 9\)
\(x\) | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
\(f\left( x \right)\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |

a) \(f\left( 1 \right) = 3.1 = 3;f\left( { - 2} \right) = 3.\left( { - 2} \right) = - 6;f\left( {\dfrac{1}{3}} \right) = 3.\dfrac{1}{3} = 1\).
b) Ta có: \(f\left( { - 3} \right) = 3.\left( { - 3} \right) = - 9;f\left( { - 1} \right) = 3.\left( { - 1} \right) = - 3\)
\(f\left( 0 \right) = 3.0 = 0;f\left( 2 \right) = 3.2 = 6;f\left( 3 \right) = 3.3 = 9\);
Ta lập được bảng sau
\(x\) | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
\(y\) | –9 | -6 | –3 | 0 | 3 | 6 | 9 |

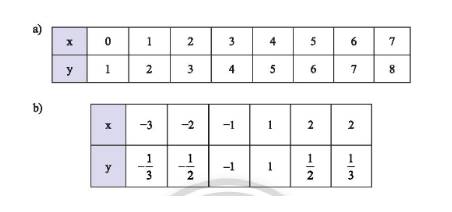
a) Bảng a đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ nhận được duy nhất một giá trị tương ứng của \(y\).
b) Bảng b đại lượng \(y\) không là hàm số của đại lượng \(x\) vì có những giá trị của \(x\) cho ta hai giá trị \(y\).
Với \(x = 2\) cho ta hai giá trị \(y\) là \(y = \dfrac{1}{2}\) và \(y = \dfrac{1}{3}\).


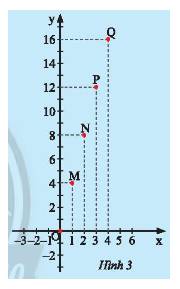
Dùng thước thẳng kiểm tra ta thấy các điểm \(O;M;N;P;Q\) thẳng hàng.

a) Ta có:
\(f\left( {\dfrac{1}{5}} \right) = \dfrac{5}{{4.\dfrac{1}{5}}} = \dfrac{5}{{\dfrac{4}{5}}} = 5:\dfrac{4}{5} = 5.\dfrac{5}{4} = \dfrac{{25}}{4};\)
\(f\left( { - 5} \right) = \dfrac{5}{{4.\left( { - 5} \right)}} = \dfrac{5}{{ - 20}} = \dfrac{{ - 1}}{4};\)
\(f\left( {\dfrac{4}{5}} \right) = \dfrac{5}{{4.\dfrac{4}{5}}} = \dfrac{5}{{\dfrac{{16}}{5}}} = 5:\dfrac{{16}}{5} = 5.\dfrac{5}{{16}} = \dfrac{{25}}{{16}}\)
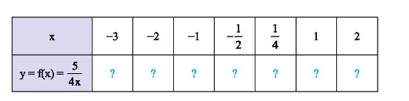
b) Ta có:
\(f\left( { - 3} \right) = \dfrac{5}{{4.\left( { - 3} \right)}} = \dfrac{5}{{ - 12}} = \dfrac{{ - 5}}{{12}};\)
\(f\left( { - 2} \right) = \dfrac{5}{{4.\left( { - 2} \right)}} = \dfrac{5}{{ - 8}} = \dfrac{{ - 5}}{8};\)
\(f\left( { - 1} \right) = \dfrac{5}{{4.\left( { - 1} \right)}} = \dfrac{5}{{ - 4}} = \dfrac{{ - 5}}{4};\)
\(f\left( { - \dfrac{1}{2}} \right) = \dfrac{5}{{4.\left( { - \dfrac{1}{2}} \right)}} = \dfrac{5}{{\dfrac{{ - 4}}{2}}} = \dfrac{5}{{ - 2}} = \dfrac{{ - 5}}{2}\);
\(f\left( {\dfrac{1}{4}} \right) = \dfrac{5}{{4.\dfrac{1}{4}}} = \dfrac{5}{{\dfrac{4}{4}}} = \dfrac{5}{1} = 5\);
\(f\left( 1 \right) = \dfrac{5}{{4.1}} = \dfrac{5}{4}\);
\(f\left( 2 \right) = \dfrac{5}{{4.2}} = \dfrac{5}{8}\)
Ta có bảng sau:
\(x\) | –3 | –2 | –1 | \( - \dfrac{1}{2}\) | \(\dfrac{1}{4}\) | 1 | 2 |
\(y = f\left( x \right) = \dfrac{5}{{4x}}\) | \(\dfrac{{ - 5}}{{12}}\) | \(\dfrac{{ - 5}}{8}\) | \(\dfrac{{ - 5}}{4}\) | \(\dfrac{{ - 5}}{2}\) | 5 | \(\dfrac{5}{4}\) | \(\dfrac{5}{8}\) |

a)
- Với \(x = - 2 \Rightarrow f\left( { - 2} \right) = - 2;g\left( { - 2} \right) = - 2 + 3 = 1\);
- Với \(x = - 1 \Rightarrow f\left( { - 1} \right) = - 1;g\left( { - 1} \right) = - 1 + 3 = 2\);
- Với \(x = 0 \Rightarrow f\left( 0 \right) = 0;g\left( 0 \right) = 0 + 3 = 3\);
- Với \(x = 1 \Rightarrow f\left( 1 \right) = 1;g\left( 1 \right) = 1 + 3 = 4\);
- Với \(x = 2 \Rightarrow f\left( 2 \right) = 2;g\left( 2 \right) = 2 + 3 = 5\);
Ta có bảng sau:
\(x\) | –2 | –1 | 0 | 1 | 2 |
\(y = f\left( x \right) = x\) | –2 | –1 | 0 | 1 | 2 |
\(y = g\left( x \right) = x + 3\) | 1 | 2 | 3 | 4 | 5 |
b)
- Vẽ đồ thị hàm số \(y = f\left( x \right) = x\)
Cho \(x = 1 \Rightarrow y = f\left( x \right) = 1\). Ta vẽ điểm \(A\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;1} \right)\).
- Các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) trong bảng trên là \(B\left( { - 2;1} \right);C\left( { - 1;2} \right);D\left( {0;3} \right);E\left( {1;4} \right);F\left( {2;5} \right)\).
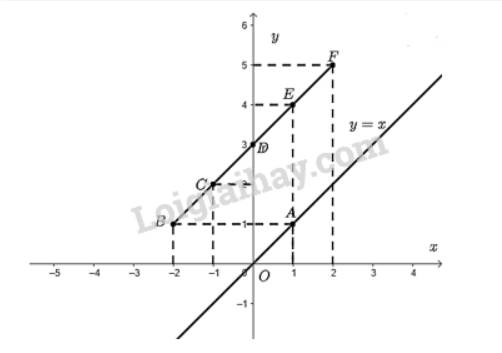
c) Ta đặt thước thẳng kiểm tra thì thấy các điểm thuộc đồ thị hàm số \(y = g\left( x \right) = x = 3\) thẳng hàng với nhau.
Dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\):
Bước 1: Chọn hai điểm \(A;B\) phân biệt thuộc đồ thị hàm số \(y = g\left( x \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(A;B\).
Đồ thị hàm số \(y = g\left( x \right)\) là đường thẳng đi qua hai điểm \(A;B\).
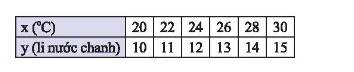
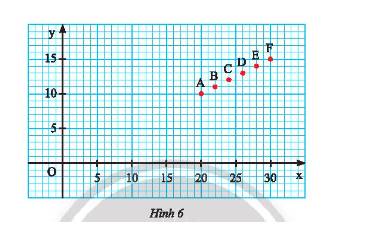






a) Điểm \(A\left( {20;10} \right);B\left( {22;11} \right);C\left( {24;12} \right);D\left( {26;13} \right);E\left( {28;14} \right);D\left( {30;15} \right)\)
Ta thấy mỗi cặp giá trị \(x;y\) tương ứng trong bảng là tọa độ của các điểm \(A;B;C;D;E;F\).