Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

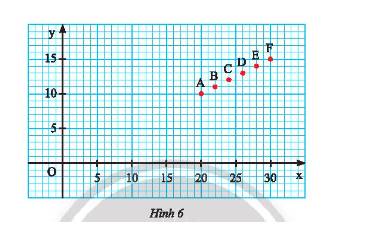
Vì đường thẳng \(d:y = mx\) đi qua các điểm \(A;B;C;D;E;F\) nên ta chọn \(A\left( {20;10} \right)\) thay vào đường thẳng ta được:
\(10 = 20.m \Leftrightarrow m = 10:20 \Leftrightarrow m = \dfrac{1}{2}\)
Do đó đường thẳng cần tìm là: \(y = \dfrac{1}{2}x\).
Hệ số góc của đường thẳng là \(a = \dfrac{1}{2}\).

a) Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2; - 6} \right);\left( { - 1; - 3} \right);\left( {0;0} \right);\left( {1;3} \right);\left( {2;6} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây
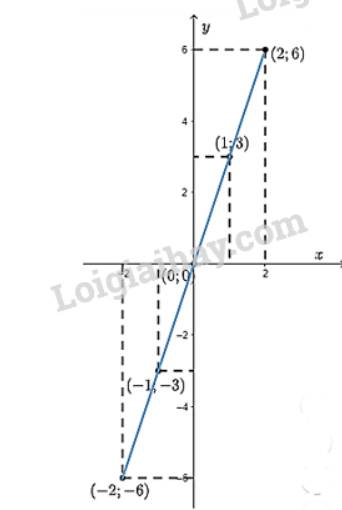
b) Các điểm vừa xác định được ở câu a đều nằm trên một đường thẳng.

a) Ứng với mỗi giờ chỉ đọc được một số chỉ nhiệt độ.
Ứng với 7h thì nhiệt độ là \(36^\circ C\)
Ứng với 8h thì nhiệt độ là \(37^\circ C\)
Ứng với 9h thì nhiệt độ là \(36^\circ C\)
Ứng với 10h thì nhiệt độ là \(37^\circ C\)
Ứng với 11h thì nhiệt độ là \(38^\circ C\)
Ứng với 12h thì nhiệt độ là \(37^\circ C\)
Ứng với 13h thì nhiệt độ là \(38^\circ C\)
Ứng với 14h thì nhiệt độ là \(39^\circ C\)
Ứng với 15h thì nhiệt độ là \(39^\circ C\)
b) Với \(v = 10 \Rightarrow t = \dfrac{{180}}{{10}} = 18\)
Với \(v = 20 \Rightarrow t = \dfrac{{180}}{{20}} = 9\)
Với \(v = 30 \Rightarrow t = \dfrac{{180}}{{30}} = 6\)
Với \(v = 60 \Rightarrow t = \dfrac{{180}}{{60}} = 3\)
Với \(v = 180 \Rightarrow t = \dfrac{{180}}{{180}} = 1\)
Lập bảng:
\(v\) | 10 | 20 | 30 | 60 | 180 |
\(t\) | 18 | 9 | 6 | 3 | 1 |

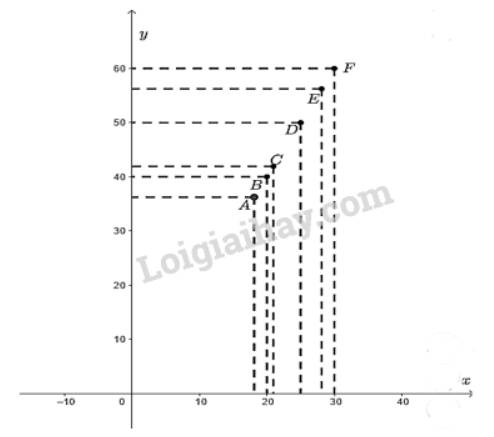
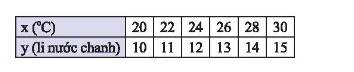
a) Điểm \(A\left( {20;10} \right);B\left( {22;11} \right);C\left( {24;12} \right);D\left( {26;13} \right);E\left( {28;14} \right);D\left( {30;15} \right)\)
Ta thấy mỗi cặp giá trị \(x;y\) tương ứng trong bảng là tọa độ của các điểm \(A;B;C;D;E;F\).

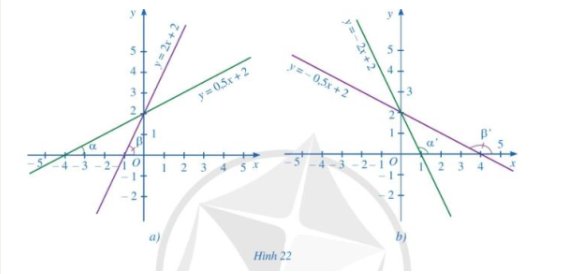
a) Quan sát hình 22a ta thấy: \(\widehat \alpha < \widehat \beta \)
- Hệ số x của hàm số y = 0,5x + 2 là 0,5
- Hệ số x của hàm số y = 2x + 2 là 2
Nhận xét:
- Khi hệ số của x > 0 => góc tạo bởi đường thẳng đó với trục Ox là góc nhọn.
- Hệ số của x càng nhỏ => góc tạo bởi đường thẳng đó với trục Ox càng nhỏ.
b) Quan sât hình 22b ta thấy: \(\widehat {\alpha '} < \widehat {\beta '}\)
- Hệ số x của hàm số y = -0,5 x + 2 là -0,5
- Hệ số x của hàm số y = -2x + 2 là -2
Ta thấy: - 0,5 > -2
Nhận xét:
- Khi hệ số của x < 0 => góc tạo bởi đường thẳng đó với trục Ox là góc tù.
- Hệ số của x càng nhỏ => góc tạo bởi đường thẳng đó với trục Ox càng nhỏ.

a) Quãng được vật đi được với vận tốc 3 \(km/h\)trong khoảng thời gian \(t\) (giờ) là:
\(s = v.t = 3.t\).
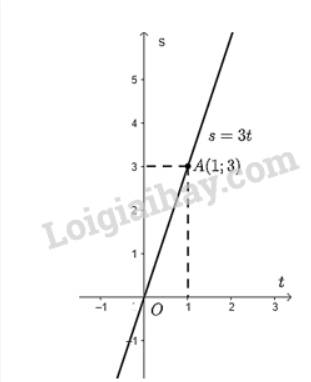
b) Vẽ đồ thị hàm số \(s = 3.t\)
Cho \(t = 1 \Rightarrow s = 3.1 = 3\)\( \Rightarrow \) đồ thị hàm số đi qua điểm \(M\left( {1;3} \right)\).
Đồ thị hàm số \(s = 3.t\) là đường thẳng đi qua hai điểm \(O\) và \(M\).

Ta có: \(C = \pi .d\) trong đó, \(C\) là chu vi đường tròn; \(d\) là đường kính và \(\pi \) là số pi.
Do đó, \(f\left( d \right) = \pi .d\)
Với \(d = 1 \Rightarrow f\left( 1 \right) = \pi .1 = \pi \);
\(d = 2 \Rightarrow f\left( 2 \right) = \pi .2 = 2\pi \);
\(d = 3 \Rightarrow f\left( 3 \right) = \pi .3 = 3\pi \);
\(d = 4 \Rightarrow f\left( 4 \right) = \pi .4 = 4\pi \).
Ta thu được bảng sau:
\(d\) | 1 | 2 | 3 | 4 |
\(f\left( d \right)\) | \(\pi \) | \(2\pi \) | \(3\pi \) | \(4\pi \) |

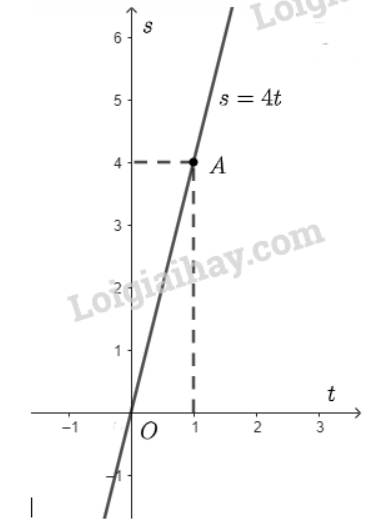
Với \(v = 4 \Rightarrow s = 4t\). Khi đó \(s\) là hàm số bậc nhất theo biến \(t\).
Với \(t = 1 \Rightarrow s = 4.1 = 4 \Rightarrow \) đồ thị hàm số đi qua điểm \(A\left( {1;4} \right)\).
Đồ thị hàm số \(s = 4t\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(A\left( {1;4} \right)\).

Theo đề số tiền 4 ngày theo thứ tự lập được một tỉ lệ thức
Gọi số tiền bán được ngày thứ tư là x
\(\Rightarrow\)\(\frac{750000}{810000}=\frac{920000}{x}\Leftrightarrow x=\frac{810000\cdot920000}{750000}=993600\)




Đồ thị hàm số là tập hợp các điểm có tọa độ \(A\left( {18;36} \right);B\left( {20;40} \right);C\left( {21;42} \right);\) \(D\left( {25;50} \right);\)\(E\left( {28;56} \right);\)\(F\left( {30;60} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây