K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 1 2018
Đầu bài sai trả bao giờ có hình nào đường chéo bằng cạnh cả!
AC=BD=12cm mới đúng! Tự làm còn lại nhé!
DT
1
O
25 tháng 3 2022
c) \(x-\dfrac{10}{3}=\dfrac{7}{15}\cdot\dfrac{3}{5}\)
\(x-\dfrac{10}{3}=\dfrac{7}{25}\)
\(x=\dfrac{7}{25}+\dfrac{10}{3}\)
\(x=\dfrac{271}{75}\)
d) \(x+\dfrac{3}{22}=\dfrac{27}{121}\div\dfrac{9}{11}\)
\(x+\dfrac{3}{22}=\dfrac{3}{11}\)
\(x=\dfrac{3}{11}-\dfrac{3}{22}\)
\(x\) \(=\dfrac{3}{22}\)
e) \(\dfrac{8}{23}\div\dfrac{24}{46}-x=\dfrac{1}{3}\)
\(\dfrac{2}{3}-x=\dfrac{1}{3}\)
\(x=\dfrac{2}{3}-\dfrac{1}{3}\)
\(x=\dfrac{1}{3}\)
f) \(1-x=\dfrac{49}{65}\cdot\dfrac{5}{7}\)
\(1-x=\dfrac{7}{13}\)
\(x=1-\dfrac{7}{13}\)
\(x=\dfrac{6}{13}\)
26 tháng 6 2021
Bài 1.2
1: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
2) Ta có: \(A=\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}+1}{3-\sqrt{x}}-\dfrac{3-11\sqrt{x}}{x-9}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{3-11\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2x-6\sqrt{x}+x+4\sqrt{x}+3-3+11\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}-3}\)
NH
0
25 tháng 8 2021
a: Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔABC
Suy ra: ED//BC và \(ED=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
M là trung điểm của GB
N là trung điểm của GC
Do đó: MN là đường trung bình của ΔGBC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\left(2\right)\)
Từ (1), (2) suy ra ED//MN và ED=MN
Xét tứ giác EMND có
ED//MN
ED=MN
Do đó: EMND là hình bình hành
b: Ta có: \(ED=\dfrac{BC}{2}\)
mà \(MN=\dfrac{BC}{2}\)
nên ED=MN
24 tháng 6 2021
`c)-x^2+7x-2=-(x^2-7x)-2`
`=-(x^2-7x+49/4-49/4)-2`
`=-(x-7/2)^2+49/4-2`
`=-(x-7/2)^2+41/4<=41/4`
Dấu "=" xảy ra khi `x=7/2`
`d)-4x^2+8x-9=-(4x^2-8x)-9`
`=-(4x^2-8x+4-4)-9`
`=-(2x-2)^2-5<=-5`
Dấu "=" xảy ra khi `x=1`
`e)-3x^2+5x+10`
`=-3(x^2-5/3x)+10`
`=-3(x^2-5/3x+25/36-25/36)+10`
`=-3(x-5/6)^2+25/12+10`
`=-3(x-5/6)^2+145/12<=145/12`
Dấu "=" xảy ra khi`x=5/6`
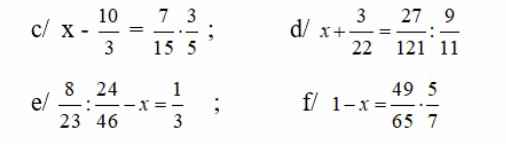
a, Để A đc xác định => 2x2- 6x \(\ne\) 0 => 2x(x-3) \(\ne\) 0 => \(\orbr{\begin{cases}x\ne0\\x\ne3\end{cases}}\). Vậy .....
b, Để A đc xác định => x2+ 1 \(\ne\) 0 => x2 \(\ne\)-1 ( luôn đúng \(\forall\)x) . Vậy A đc xđ \(\forall x\in R\)
c, Để A đc xđ => 16 - 24x + 9x2\(\ne0\)=> ( 4 - 3x )2\(\ne0\)=> \(x\ne\frac{4}{3}\).Vậy..........
d, Để A đc xđ => x2 - 3x + 2 \(\ne0\)=> ( x - 2 )( x - 1 )\(\ne0\)=> \(\orbr{\begin{cases}x\ne2\\x\ne1\end{cases}}\).Vậy .......
e,Để A đc xđ => x2 - 3x + 4\(\ne0\)=> ( x - 3/2)2 + 7/4 \(\ne0\)(( luôn đúng \(\forall\)x) . Vậy A đc xđ \(\forall x\in R\)