
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x-3\right)^2+\left|y^2-9\right|=0\)
Vì \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge0\forall x\\\left|y^2-9\right|\ge0\forall y\end{matrix}\right.\)
để bt = 0 \(\Leftrightarrow\left\{{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\y^2-9=0\Rightarrow y^2=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)
Vậy.....
\(\left(x-3\right)^2+\left|y^2-9\right|=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\y^2-9=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\y^2=9\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=3\\y=3hoặcy=-3\end{matrix}\right.\)

' Bạn j đó ơi , mấy bài này dễ , chủ yếu bạn nên mở sách giáo khoa , cái chỗ mà bày vẽ hình ý . Chúc bạn thành công :v

\(\left(x-3\right).\left(x-2015\right)< 0\)
\(\Rightarrow\left(x-3\right)và\left(x-2015\right)\) phải khác dấu
\(\Rightarrow\left(x-3\right)< \left(x-2015\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x-3>0\\x-2015< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>3\\x< 2015\end{matrix}\right.\)
\(\Rightarrow3< x< 2015\)
\(\Rightarrow x\in\left\{4;5;6;7;8;...;2013;2014\right\}\)
( ko bt đúng hay sai nx )
thám tử
\(\left(x-3\right)\left(x-2015\right)< 0\)
Với mọi \(x\in R\) thì:
\(x-2015< x-3\)
Khi đó: \(\left\{{}\begin{matrix}x-2015< 0\\x-3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 2015\\x>3\end{matrix}\right.\)
Nên \(3< x< 2015\)

Câu hỏi của Nguyễn Trọng Phúc - Toán lớp 7 | Học trực tuyến

bài 5) b)
Ta có: \(a+c=2b\)
\(\Rightarrow d\left(a+c\right)=2bd\) (1)
Ta lại có: \(2bd=c\left(b+d\right)\) (2)
Từ (1) và (2) suy ra: \(d\left(a+c\right)=c\left(b+d\right)\)
\(\Rightarrow ad+cd=bc+cd\)
\(\Rightarrow ad=bc\)
\(\Rightarrow\dfrac{a}{b}=\dfrac{c}{d}\) (đpcm)
Câu 1:D
Câu 2:D
Câu 3:B
Câu 4:D
Câu 5:C
Câu 6:C
Câu 7:D
Câu 8:A

\(\left|x-\dfrac{1}{2}\right|+\left|y+\dfrac{2}{3}\right|+\left|x^2+xz\right|=0\)
\(\left\{{}\begin{matrix}\left|x-\dfrac{1}{2}\right|\ge0\forall x\\\left|y+\dfrac{2}{3}\right|\ge0\forall y\\\left|x^2+xz\right|\ge0\forall x;z\end{matrix}\right.\) \(\Rightarrow\left|x-\dfrac{1}{2}\right|+\left|y+\dfrac{2}{3}\right|+\left|x^2+xz\right|\ge0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\left|x-\dfrac{1}{2}\right|=0\\\left|y+\dfrac{2}{3}\right|=0\\\left|x^2+xz\right|=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-\dfrac{2}{3}\\z=-\dfrac{1}{2}\end{matrix}\right.\)

\(x-y=9\Rightarrow x=9+y\Rightarrow y=x-9\)
Ta có:
\(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\)
\(=\dfrac{3x+x-9}{3x+y}-\dfrac{3y+y+9}{3y+x}\)
\(=\dfrac{3x+\left(x-9\right)}{3x+y}-\dfrac{3y+\left(y+9\right)}{3y+x}\)
\(=\dfrac{3x+y}{3x+y}-\dfrac{3y+x}{3y+x}\)
\(=1-1\)
\(=0\)
Vậy biểu thức \(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\)khi \(x-y=9\) là 0
\(x-y=9\Rightarrow y=x-9\) thay vào biểu thức B ta được :
\(B=\dfrac{4x-9}{3x+\left(x-9\right)}-\dfrac{4\left(x-9\right)+9}{3\left(x-9\right)+x}=\dfrac{4x-9}{4x-9}-\dfrac{4x-27}{4x-27}=1-1=0\)
Vậy giá trị của B là 0 tại \(x-y=9\)

Bài 1:
A B C . . / D E F / // // x x
a) Xét \(\Delta AED\) và \(\Delta CEF\)có:
AE = EC (gt)
\(\widehat{AED}=\widehat{CEF}\left(đđ\right)\)
DE = EF (gt)
Do đó: \(\Delta AED=\Delta CEF\left(c-g-c\right)\)
=> AD = CF (hai cạnh tương ứng)
mà AD = DB (D là trung điểm của BA)
=> CF = DB
b) Vì \(\Delta AED=\Delta CEF\left(c-g-c\right)\)
=> \(\widehat{DAE}=\widehat{FCE}\) (hai cạnh tương ứng)
=> DA // CF
mà D nằm giữa đoạn thẳng AB (D là trung điểm của AB)
=> DB // CF
=> \(\widehat{BDC}=\widehat{FCD}\left(soletrong\right)\)
Xét \(\Delta BDC\) và \(\Delta FCD\) có:
DC (chung)
\(\widehat{BDC}=\widehat{FCD}\left(cmt\right)\)
BD = CF (cmt)
Do đó: \(\Delta BDC=\Delta FCD\left(c-g-c\right)\)
c) Vì \(\Delta BDC=\Delta FCD\left(cmt\right)\)
=> \(\widehat{BCD}=\widehat{FCD}\) (hai cạnh tương ứng)
=> DF // BC (soletrong)
hay DE // BC
Vì \(\Delta BDC=\Delta FCD\left(cmt\right)\)
=> DF = BC (hai cạnh tương ứng)
mà \(DE=\dfrac{1}{2}DF\) (D là trung điểm của DF)
=> \(DE=\dfrac{1}{2}BC\)

Em vào đây nhé Vẽ hình trực tuyến trên hoc24 | Hướng dẫn tạo khóa học trên hoc24 | Học trực tuyến
Vẽ hình trực tuyến trên hoc24 | Hướng dẫn tạo khóa học trên hoc24 | Học trực tuyến
Ấn vào cái chữ màu xanh nhé!
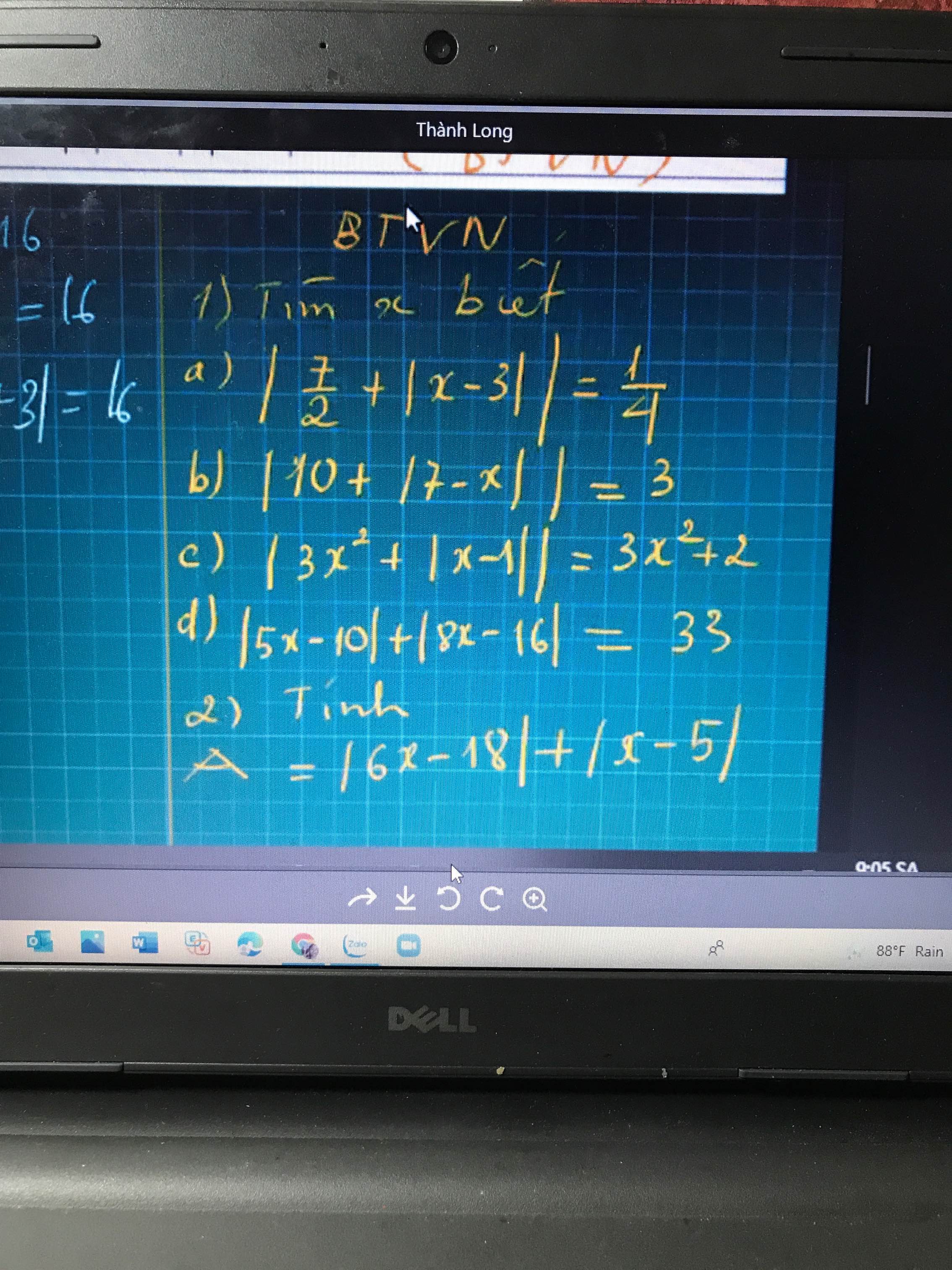




 GIÚP VỚI CẦN GẤP LẮM !!!
GIÚP VỚI CẦN GẤP LẮM !!! 

b: Ta có: |10+|7-x||=3
\(\Leftrightarrow\left[{}\begin{matrix}\left|x-7\right|+10=-3\\\left|x-7\right|+10=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left|x-7\right|=-13\left(vôlý\right)\\\left|x-7\right|=-7\left(vôlý\right)\end{matrix}\right.\)