
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






1. Xét hai tam giác \(PNA\)và \(MNC\):
\(\widehat{PNA}=\widehat{MNC}\)(hai góc đối đỉnh)
\(AN=NC\)
\(\widehat{NCM}=\widehat{NAP}\)(hai góc so le trong)
Suy ra \(\Delta PNA=\Delta MNC\left(g.c.g\right)\)
2. Xét tứ giác \(APCM\)có: \(AP//MC,AP=CM\)
do đó \(APCM\)là hình bình hành.
Suy ra \(PC=AM\).
Xét tam giác \(ABC\)có \(AB=AC\)nên tam giác \(ABC\)cân tại \(A\)
do đó trung tuyến \(AM\)đồng thời là đường cao của tam giác \(ABC\)
\(\Rightarrow AM\perp BC\)
\(APCM\)là hình bình hành nên \(PC//AM\)
suy ra \(PC\perp BC\).
3. Xét tam giác \(AIP\)và tam giác \(MIB\):
\(\widehat{API}=\widehat{MBI}\)(hai góc so le trong)
\(BM=AP\left(=MC\right)\)
\(\widehat{PAI}=\widehat{BMI}\left(=90^o\right)\)
suy ra \(\Delta AIP=\Delta MIB\left(g.c.g\right)\)
4. \(\Delta AIP=\Delta MIB\Rightarrow AI=MI\)
suy ra \(I\)là trung điểm của \(AM\).
Xét tam giác \(AMC\):
\(I,N\)lần lượt là trung điểm của \(AM,AC\)nên \(IN\)là đường trung bình của tam giác \(AMC\)
suy ra \(IN//BC\).

Đặt mắt ở một đầu thước, đầu kia của thước hướng về một nguồn sáng, nhìn dọc theo thước. Điều chỉnh hướng của thước sao cho điểm đầu của cạnh thước ở phía mắt che khuất điểm đầu kia của cạnh thước. Nếu tất cả các điểm trên cạnh thước cũng đều bị che khuất thì cạnh thước thẳng. Lí do là vì tia sáng phát ra từ nguồn đi theo một đường thẳng bị đầu thước gần nguồn chặn lại nên không đến được các điểm khác cũng nằm trên đường thẳng ấy trên cạnh thước để đến mắt.

 Giúp mình với ạ, mình cảm ơn nhiều
Giúp mình với ạ, mình cảm ơn nhiều
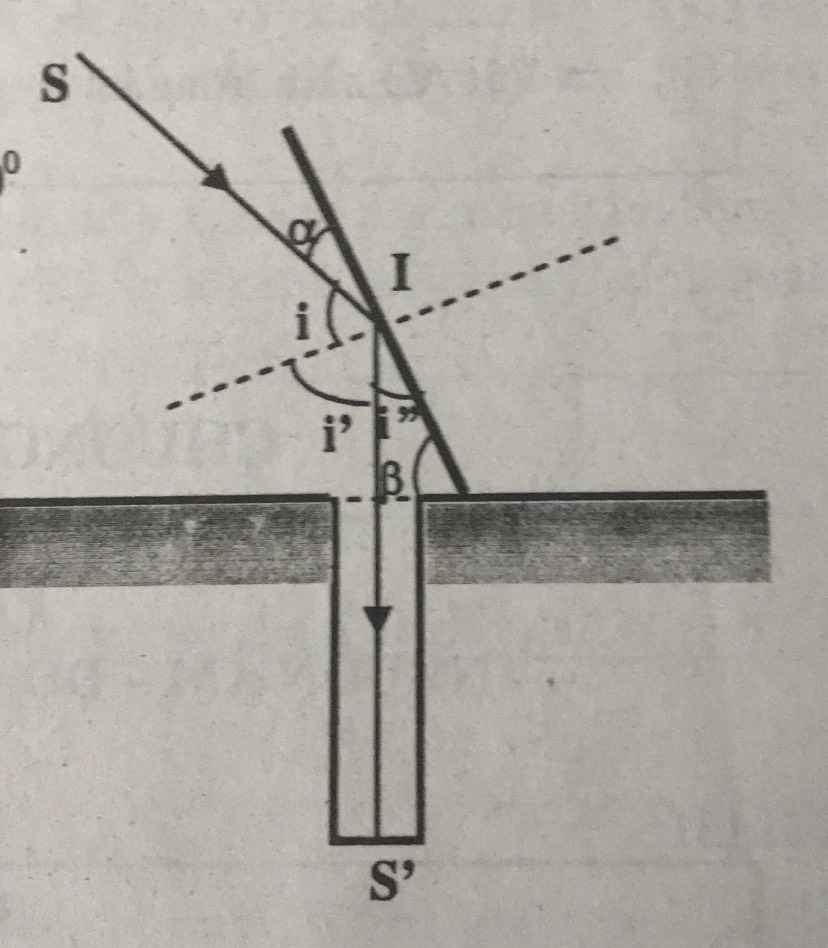 Mọi người giúp mình với ạ! Mình cảm ơn nhiều ạ!
Mọi người giúp mình với ạ! Mình cảm ơn nhiều ạ!

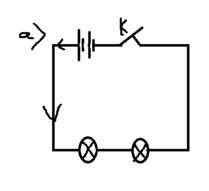
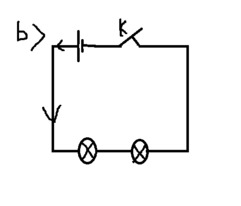
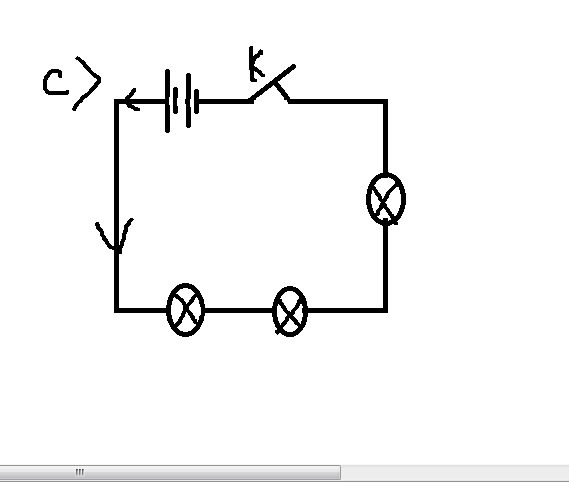

bài 1:
a)30 độ
b)55 độ
bài 2:
Góc tới bằng 35 độ
bài 3:bạn tự vẽ và tự làm, bài không khó đâu
Câu 1:
a/120 độ.
b/70 độ.
Câu 2:
-Góc tới bằng 35 độ.