K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 3 2023
\(S_{Xq}=2\cdot pi\cdot2^2+\dfrac{1}{2}\cdot\sqrt{5}\cdot2=3\sqrt{5}\cdot pi\)
XO
4 tháng 4 2022
ĐK : x \(\ge-1\)
Ta có : \(x^2-2x-1=\sqrt{\left(x^2+1\right)\left(x+1\right)}\)
<=> \(\left(x^2+1\right)-2\left(x+1\right)=\sqrt{\left(x^2+1\right)\left(x+1\right)}\)
Đặt \(\sqrt{x^2+1}=a;\sqrt{x+1}=b\)(\(a>0;b\ge0\))
Khi đó a2 - 2b2 = ab
<=> (a - 2b)(a + b) = 0
<=> a - 2b = 0
<=> a = 2b
<=> \(\sqrt{x^2+1}=2\sqrt{x+1}\)
<=> \(\left\{{}\begin{matrix}x^2+1=4x+4\\x\ge-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-4x-3=0\\x\ge-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=\sqrt{7}+2\\x=-\sqrt{7}+2\end{matrix}\right.\\x\ge-1\end{matrix}\right.\Leftrightarrow x=\sqrt{7}+2\)
5 tháng 1 2022
a: =>x=y+11
xy=60
=>y(y+11)=60
\(\Leftrightarrow y^2+15y-4y-60=0\)
=>(y+15)(y-4)=0
hay \(y\in\left\{-15;4\right\}\)
6 tháng 3 2023
10: =>1/2x=3/4 và x+y=2
=>x=3/4*2=3/2 và y=1/2
11:=>4x+5y=3 và 4x-12y=20
=>17y=-17 và x-3y=5
=>y=-1 và x=3y+5=-3+5=2
12: =>7x-2y=1 và 6x+2y=12
=>13x=13 và 3x+y=6
=>x=1 và y=3
13:=>2/x=1 và 1/x-1/y=1/5
=>x=2 và 1/y=1/2-1/5=3/10
=>y=10/3 và x=2
14: =>12/x-16/y=8 và 12/x-15/y=9
=>-1/y=-1 và 4/x-5/y=3
=>y=1 và 4/x=3+5=8
=>x=1/2 và y=1
3 tháng 3 2023
Bài 9:
a: a=1; b=-2m; c=-1
Vì a*c<0
nên (1) luôn có 2 nghiệm pb
b: x1^2+x2^2-x1x2=7
=>(x1+x2)^2-3x1x2=7
=>(2m)^2-3*(-1)=7
=>4m^2+3=7
=>m=1 hoặc m=-1
3 tháng 3 2023
a: Khi m=3 thì (1): x^2-6x+4=0
=>x^2-6x+9-5=0
=>(x-3)^2=5
=>\(x=3\pm\sqrt{5}\)
NA
1
12 tháng 10 2021
a: \(\sqrt{252}+\dfrac{1}{3}\sqrt{63}-\sqrt{175}\)
\(=4\sqrt{7}+\sqrt{7}-5\sqrt{7}\)
=0
AN
1
4 tháng 3 2023
a: Δ=(m-2)^2-4(m-4)
=m^2-4m+4-4m+16
=m^2-8m+20
=m^2-8m+16+4
=(m-2)^2+4>=4>0
=>Phương trình luôn có 2 nghiệm pb
b: x1^2+x2^2
=(x1+x2)^2-2x1x2
=(m-2)^2-2(m-4)
=m^2-4m+4-2m+8
=m^2-6m+12
=(m-3)^2+3>=3
Dấu = xảy ra khi m=3
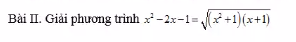
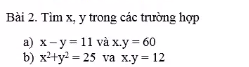
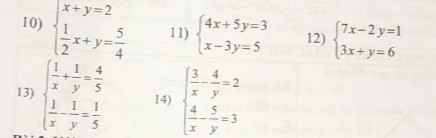
R=1/2CD=a
h=AD=2a
S1=Sxq=2*pi*r*h=2*pi*a*2a=4*pi*a^2
S2=Stp=2*pi*r^2+2*pi*r*h
=2*pi*a^2+2*pi*a*2a
=6*pi*a^2
>S1/S2=2/3