
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 6:
Gọi độ dài hai cạnh lần lượt là a,b
Theo đề, ta có: a/3=b/5 và a+b=24
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{a+b}{3+5}=\dfrac{24}{8}=3\)
=>a=9; b=15

Câu 3:
a: Xét ΔABC có AB<BC
nên \(\widehat{ACB}< \widehat{BAC}\)
b: Xét ΔABM có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABM cân tại A
mà \(\widehat{B}=60^0\)
nên ΔABM đều

5)gọi Cx là tia đối tia CA
Ta có ˆCAH=ˆCBACAH^=CBA^
và ˆACH=ˆBCAACH^=BCA^
=>△CAH∼△CBA△CAH∼△CBA (g, g)
=>CHCA=AHBACHCA=AHBA (1)
có AE là phân giác BAH
=>AHAB=EHEBAHAB=EHEB (2)
Áp dụng Menelauyt cho 3 điểm E, M, F và tam giác HAB ta có
EHEB.MBMA.FAFH=1EHEB.MBMA.FAFH=1
<=>EHEB=FHFAEHEB=FHFA (3)
từ (1, 2, 3) =>CHCA=FHFACHCA=FHFA (4)
mà F thẳng hàng với H, A và nằm ngoài đoạn thẳng HA (5)
từ (4, 5) =>CF là phân giác ngoài góc ACB
=>ˆBCF=12.ˆBCx=12.(ˆBAC+ˆABC)BCF^=12.BCx^=12.(BAC^+ABC^) (6)
mặt khác ˆAEC=ˆABC+ˆEABAEC^=ABC^+EAB^
=ˆABC+12.ˆBAH=ABC^+12.BAH^
=ˆABC+12.(ˆBAC−ˆABC)=ABC^+12.(BAC^−ABC^)
=12.(ˆBAC+ˆABC)=12.(BAC^+ABC^) (7)
từ (6, 7) =>ˆBCF=ˆAECBCF^=AEC^
=>CF //AE (đpcm)

\(5,\\ 5\cdot625=25\cdot125\\ \Leftrightarrow\dfrac{5}{25}=\dfrac{125}{625};\dfrac{5}{125}=\dfrac{25}{625};\dfrac{625}{25}=\dfrac{125}{5};\dfrac{625}{125}=\dfrac{25}{5}\)
\(6,\)
\(a,\) Áp dụng t/c dtsbn: \(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{-21}{7}=-3\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-3\cdot2=-6\\y=-3\cdot5=-15\end{matrix}\right.\)
\(b,7x=3y\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{7}\)
Áp dụng t/c dtsbn: \(\dfrac{x}{3}=\dfrac{y}{7}=\dfrac{x-y}{3-7}=\dfrac{16}{-4}=-4\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-4\cdot3=-12\\y=-4\cdot7=-28\end{matrix}\right.\)
\(7,\\ a:b:c:d=2:3:4:5\Leftrightarrow\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{d}{5}\)
Áp dụng t/c dtsbn: \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{d}{5}=\dfrac{a+b+c+d}{2+3+4+5}=\dfrac{-42}{14}=-3\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-3\cdot2=-6\\b=-3\cdot3=-9\\c=-3\cdot4=-12\\d=-3\cdot5=-15\end{matrix}\right.\)

\(5,\\ \left\{{}\begin{matrix}AB\perp AD\\CD\perp AD\end{matrix}\right.\Rightarrow AB//CD\\ \Rightarrow\widehat{ABC}+\widehat{BCD}=180^0\left(2.góc.TCP\right)\\ \Rightarrow60^0+\widehat{BCD}=180^0\\ \Rightarrow\widehat{BCD}=120^0\)
\(6,\\ a,\left\{{}\begin{matrix}a\perp AB\\a//b\end{matrix}\right.\Rightarrow b\perp AB\\ b,a//b\Rightarrow\widehat{C}+\widehat{D}=180^0\left(2.góc.TCP\right)\\ \Rightarrow\widehat{D}=180^0-120^0=60^0\\ c,\widehat{ICD}=\dfrac{1}{2}\widehat{ACD}=\dfrac{1}{2}\cdot120^0=60^0\left(t/c.phân.giác\right)\\ \Delta CID.có:\widehat{CID}+\widehat{IDC}+\widehat{ICD}=180^0\\ \Rightarrow60^0+60^0+\widehat{CID}=180^0\\ \Rightarrow\widehat{CID}=60^0\)

Lời giải:
$BC\parallel AD$ nên $\widehat{C}+\widehat{D}=180^0$ (hai góc trong cùng phía)
$\Rightarrow \widehat{D}=180^0-\widehat{C}=180^0-73^0=107^0$
Vì $AB\parallel CD$ nên $\widehat{B}+\widehat{C}=180^0$ (trong cùng phía)
$\Rightarrow \widehat{B}=180^0-\widehat{C}=180^0-73^0=107^0$
$\widehat{A}+\widehat{D}=180^0$ (trong cùng phía)
$\Rightarrow \widehat{A}=180^0-\widehat{D}=180^0-107^0=73^0$
Bài 3: Không có ký hiệu góc. Bạn cần bổ sung thêm
Bài 4:
Vì $AB\parallel CD$ nên:
$\widehat{ACD}+\widehat{BAC}=180^0$ (hai góc trong cùng phía)
$\widehat{ACD}=180^0-\widehat{BAC}=180^0-40^0=140^0$
b.
$AB\parallel CD$ nên:
$\widehat{ACH}=\widehat{CAB}=40^0$ (so le trong)
$CD\parallel EG$ nên:
$\widehat{HCE}=\widehat{CEG}=50^0$ (so le trong)
$\Rightarrow \widehat{ACH}+\widehat{HCE}=40^0+50^0$
Hay $\widehat{ACE}=90^0$

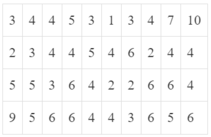
Trong bài số liệu ban đầu có 40 giá trị. Vậy có 40 bạn làm bài

a: M(x)+N(x)=7x^3-8x^2-13x-7
b: M(x)+Q(x)=12x^3-2x^2-5x-20
c: N(x)+Q(x)=13x^3-22x-9
d: N(x)-Q(x)=-5x^3-6x^2-8x+13
e: Q(x)-M(x)=6x^3+8x^2-9x-2

Gọi chiều dài và chiều rộng lần lượt là x, y
Vì tỉ số giữa chiều dài và chiều rộng là \(\frac{2}{5}\) nên
\(\frac{x}{y}\)= \(\frac{2}{5}\)suy ra \(\frac{x}{5}\)= \(\frac{y}{2}\)
Vì chu vi hình mảnh đất hình chữ nhật là 70 nên
2*( x+y ) = 70
suy ra x+y=70/2=35
Áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{x}{5}\)= \(\frac{y}{2}\)= \(\frac{x+y}{5+2}=\frac{35}{7}=5\)
\(\frac{x}{5}=5\Rightarrow x=2\cdot5=25\)
\(\frac{y}{2}=5\Rightarrow y=2\cdot5=10\)
Diện tích 25*10=250m2
Vậy diện tích mảnh đất hình chữ nhật là 250m2









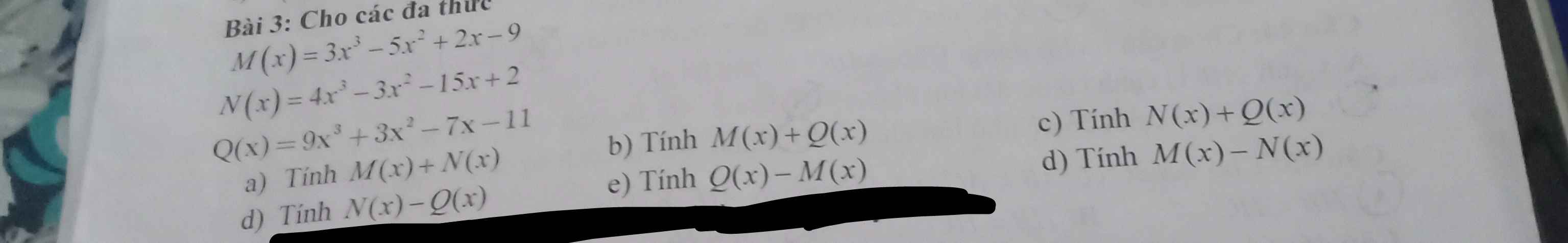
??????????????????????????