
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


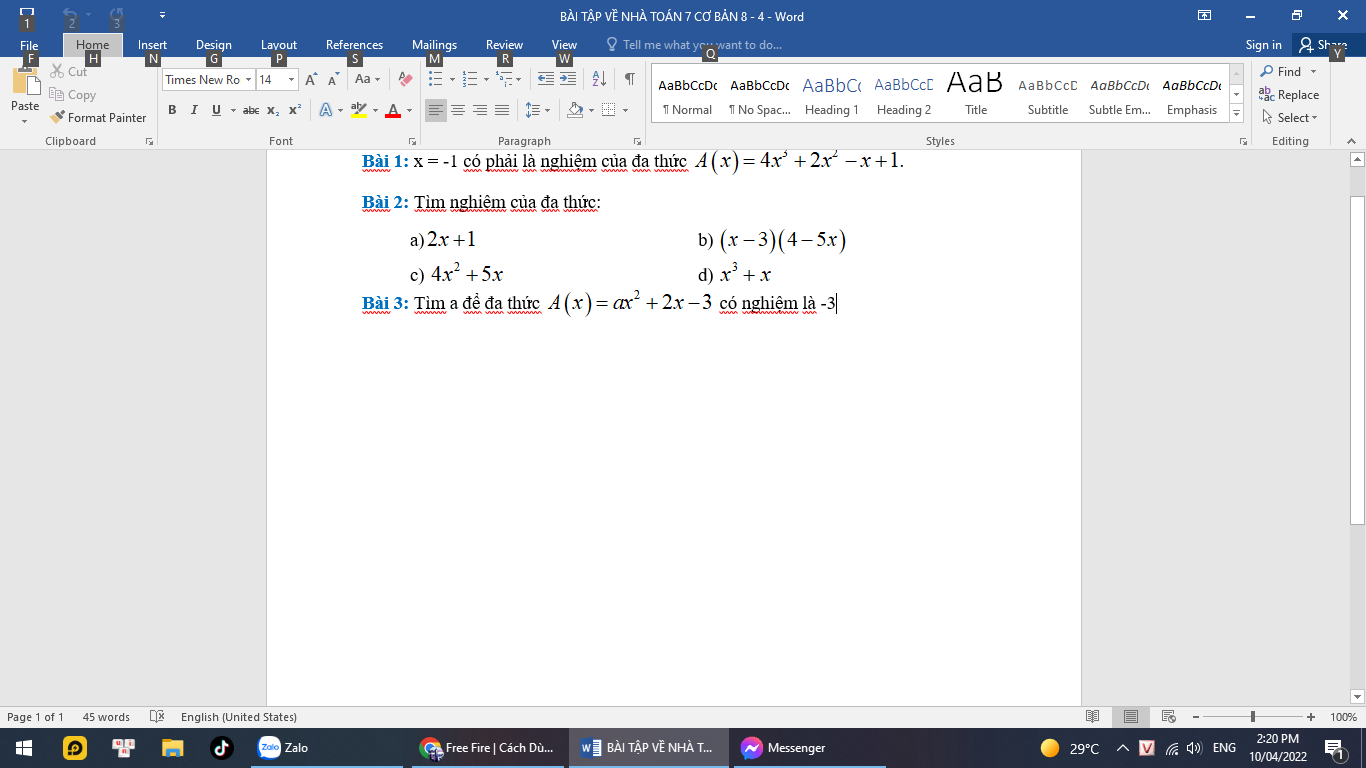
Do đa thức A(x) có nghiệm là -3
\(\Leftrightarrow A\left(-3\right)=0\)
\(\Leftrightarrow a.\left(-3\right)^2+2.\left(-3\right)-3=0\)
\(\Leftrightarrow9a-9=0\)
\(\Leftrightarrow a=1\)

Bài 2:
a) \(\dfrac{2}{15}-\dfrac{7}{10}=\dfrac{4}{30}-\dfrac{21}{30}=-\dfrac{17}{30}\)
b) \(\dfrac{-3}{14}+\dfrac{2}{21}=\dfrac{-9}{42}+\dfrac{4}{42}=\dfrac{-5}{42}\)
c) \(\dfrac{-6}{9}+\dfrac{-12}{16}=\dfrac{-96}{144}+\dfrac{-108}{144}=\dfrac{-204}{144}=-\dfrac{17}{12}\)
Bài 3:
a) \(\dfrac{3}{8}+\dfrac{-5}{6}=\dfrac{3}{8}-\dfrac{5}{6}=\dfrac{18}{48}-\dfrac{40}{48}=-\dfrac{22}{48}=-\dfrac{11}{24}\)
b) \(\dfrac{-8}{18}-\dfrac{15}{27}=\dfrac{-24}{54}-\dfrac{30}{54}=\dfrac{-54}{54}=-1\)
c) \(\dfrac{2}{21}-\dfrac{-1}{28}=\dfrac{8}{84}-\dfrac{-3}{84}=\dfrac{11}{84}\)

Câu 3:
a: Xét ΔABC có AB<BC
nên \(\widehat{ACB}< \widehat{BAC}\)
b: Xét ΔABM có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABM cân tại A
mà \(\widehat{B}=60^0\)
nên ΔABM đều

\(5,\\ 5\cdot625=25\cdot125\\ \Leftrightarrow\dfrac{5}{25}=\dfrac{125}{625};\dfrac{5}{125}=\dfrac{25}{625};\dfrac{625}{25}=\dfrac{125}{5};\dfrac{625}{125}=\dfrac{25}{5}\)
\(6,\)
\(a,\) Áp dụng t/c dtsbn: \(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{-21}{7}=-3\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-3\cdot2=-6\\y=-3\cdot5=-15\end{matrix}\right.\)
\(b,7x=3y\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{7}\)
Áp dụng t/c dtsbn: \(\dfrac{x}{3}=\dfrac{y}{7}=\dfrac{x-y}{3-7}=\dfrac{16}{-4}=-4\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-4\cdot3=-12\\y=-4\cdot7=-28\end{matrix}\right.\)
\(7,\\ a:b:c:d=2:3:4:5\Leftrightarrow\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{d}{5}\)
Áp dụng t/c dtsbn: \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{d}{5}=\dfrac{a+b+c+d}{2+3+4+5}=\dfrac{-42}{14}=-3\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-3\cdot2=-6\\b=-3\cdot3=-9\\c=-3\cdot4=-12\\d=-3\cdot5=-15\end{matrix}\right.\)

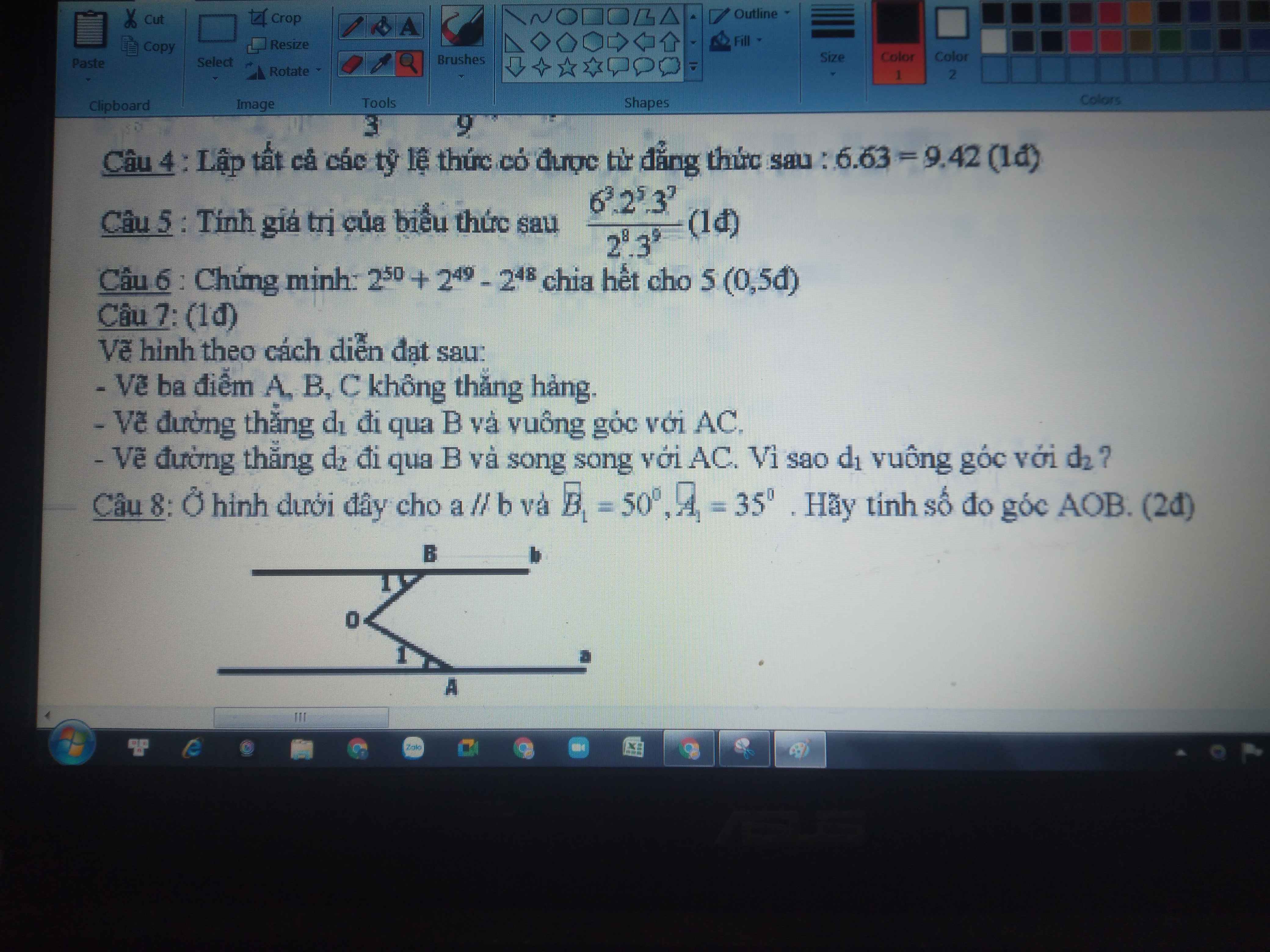
\(5,\\ \left\{{}\begin{matrix}AB\perp AD\\CD\perp AD\end{matrix}\right.\Rightarrow AB//CD\\ \Rightarrow\widehat{ABC}+\widehat{BCD}=180^0\left(2.góc.TCP\right)\\ \Rightarrow60^0+\widehat{BCD}=180^0\\ \Rightarrow\widehat{BCD}=120^0\)
\(6,\\ a,\left\{{}\begin{matrix}a\perp AB\\a//b\end{matrix}\right.\Rightarrow b\perp AB\\ b,a//b\Rightarrow\widehat{C}+\widehat{D}=180^0\left(2.góc.TCP\right)\\ \Rightarrow\widehat{D}=180^0-120^0=60^0\\ c,\widehat{ICD}=\dfrac{1}{2}\widehat{ACD}=\dfrac{1}{2}\cdot120^0=60^0\left(t/c.phân.giác\right)\\ \Delta CID.có:\widehat{CID}+\widehat{IDC}+\widehat{ICD}=180^0\\ \Rightarrow60^0+60^0+\widehat{CID}=180^0\\ \Rightarrow\widehat{CID}=60^0\)

 ai giải dùm em bài cuối vs
ai giải dùm em bài cuối vs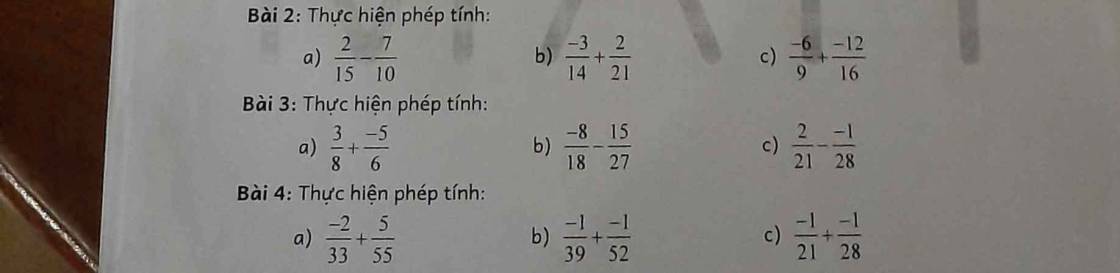






Bài 6:
Gọi độ dài hai cạnh lần lượt là a,b
Theo đề, ta có: a/3=b/5 và a+b=24
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{a+b}{3+5}=\dfrac{24}{8}=3\)
=>a=9; b=15