K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KS
2
23 tháng 6 2017
1) \(x^3-1=x^3-1^3=\left(x-1\right)\left(x^2+x+1\right)\)
2) \(27x^3-64=\left(3x\right)^3-4^3=\left(3x-4\right)\left(9x^2+12x+4\right)\)
3) \(8x^3+1=\left(2x\right)^3+1^3=\left(2x+1\right)\left(4x^2-2x+1\right)\)
TB
0
K
1
Q
23 tháng 6 2017
1) \(\left(3x-2a\right)^3\)
\(=\left(3x\right)^3-3\left(3x\right)^2\cdot2a+3\cdot3x\cdot\left(2a\right)^2-\left(2a\right)^3\)
\(=27x^3-3\cdot9x^2\cdot2a+3\cdot3x\cdot4a^2-8a^3\)
\(=27x^3-54ax^2+36a^2x-8a^3\)
2) \(\left(\dfrac{x+y}{3}\right)^3\)
\(=\dfrac{\left(x+y\right)^3}{27}\)
\(=\dfrac{x^3+3x^2y+3xy^2+y^3}{27}\)
3) \(\left(3x+\dfrac{y}{3}\right)^3\)
\(=\dfrac{\left(3x+y\right)^3}{27}\)
\(=\dfrac{27x^3+27x^2y+9xy^2+y^3}{27}\)
A
2
DT
3
DT
14 tháng 5 2017
Ngoài những hằng đẳng thức cơ bản trong sgk, còn có những hằng đẳng thức hay được sử dụng trong các bài toán như sau:
(1) (a+b+c)2=a2+b2+c2+2ab+2bc+2ac(a+b+c)2=a2+b2+c2+2ab+2bc+2ac
(2) (a+b−c)2=a2+b2+c2+2ab−2bc−2ac(a+b−c)2=a2+b2+c2+2ab−2bc−2ac
(3) (a−b−c)2=a2+b2+c2−2ab−2ac+2bc(a−b−c)2=a2+b2+c2−2ab−2ac+2bc
(4) a3+b3=(a+b)3−3ab(a+b)a3+b3=(a+b)3−3ab(a+b)
(5) a3−b3=(a−b)3+3ab(a−b)a3−b3=(a−b)3+3ab(a−b)
(6) (a+b+c)3=a3+b3+c3+3(a+b)(b+c)(c+a)(a+b+c)3=a3+b3+c3+3(a+b)(b+c)(c+a)
(7) a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ac)a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ac)
(8) (a−b)3+(b−c)3+(c−a)3=3(a−b)(b−c)(c−a)(a−b)3+(b−c)3+(c−a)3=3(a−b)(b−c)(c−a)
(9) (a+b)(b+c)(c+a)−8abc=a(b−c)2+b(c−a)2+c(a−b)2(a+b)(b+c)(c+a)−8abc=a(b−c)2+b(c−a)2+c(a−b)2
(10) (a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)−abc(a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)−abc
(11) ab2+bc2+ca2−a2b−b2c−c2a=(a−b)3+(b−c)3+(c−a)33ab2+bc2+ca2−a2b−b2c−c2a=(a−b)3+(b−c)3+(c−a)33
(12)ab3+bc3+ca3−a3b−b3c−c3a=(a+b+c)[(a−b)3+(b−c)3+(c−a)3]3ab3+bc3+ca3−a3b−b3c−c3a=(a+b+c)[(a−b)3+(b−c)3+(c−a)3]3
(13) an−bn=(a−b)(an−1+an−2b+an−3b2+...+a2bn−3+abn−2+bn−1)an−bn=(a−b)(an−1+an−2b+an−3b2+...+a2bn−3+abn−2+bn−1)
(14) Với n lẻ:
an+bn=(a+b)(an−1−an−2b+an−3b2−...+a2bn−3−abn−2+bn−1)an+bn=(a+b)(an−1−an−2b+an−3b2−...+a2bn−3−abn−2+bn−1)
(15) Nhị thức Newton:
(a+b)n=an+n!(n−1)!1!an−1b+n!(n−2)!2!an−2b2+...+n!(n−k)!k!an−kbk+...+n!2!(n−2)!a2bn−2+n)!1!(n−1)!abn−1+bn
DT
14 tháng 5 2017
Các hằng đẳng thức mở rộng thì nhiều nhưng quan trọng phải nhớ tốt mà biết vận dụng linh hoạt.
(a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc
(a + b - c)² = a² + b² + c² + 2ab - 2ac - 2bc
(a + b + c + d)² = a² + b² + c² + d² + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd
(a + b + c)³ = a³ + b³ + c³ + 3(a + b)(a + c)(b + c)
a³ + b³ = (a + b)³ - 3ab(a + b)
a³ - b³ = (a - b)³ + 3ab(a - b)
a^n + b^n = (a + b)( a^(n - 1) - a^(n - 2)b + ... + b^(n - 1) )
a^n - b^n = (a - b)( a^(n - 1) + a^(n - 2)b + ....+b^(n - 1) )
a³ + b³ + c³ - 3abc = (a + b + c)(a² + b² + c² - ab - ac - bc)
23 tháng 6 2022
a: \(=3x+y-z-4x+2y-6z=-x+3y-7z\)
b: \(=x^3+6x^2+5y^3-2x^3+5x-7y^3=-x^3+6x^2+5x-2y^3\)
c: \(=5.7x^2y-3.1xy+8y^3-6.9xy+2.3x^2y+8y^3\)
\(=8x^2y-10xy+16y^3\)
TT
4
19 tháng 1 2016
(a + b)n = nC0an + nC1an − 1b + nC2an − 2b2 + nC3an − 3b3 + ... + nCnbn
Đã nghĩ ra
Nhờ công thức tổ hợp và chỉnh hợp lớp 11
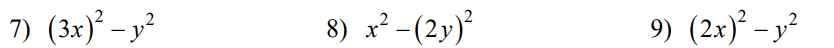
x3+8y3=x3+(2y)3=(x+2y)(x2-2xy+4y2)
P/s: Mình nghĩ vậy đó.